2025-09-10 3603 0
用于密闭和侵入颗粒介质的SPH/FEA方法
SPH/FEA method for confined and intruded granular media
摘要: 提出了一种将光滑颗粒流体力学(SPH)与有限元分析(FEA)相结合的新方法,以解决模拟颗粒介质与刚性固体相互作用中的大变形过程的计算难题。在自由表面、实体边界和SPH/有限元界面处引入虚拟粒子保持了边界和界面附近的粒子采样精度。提出的在SPH/FEA模型中应用初始应力场的方法可以模拟约束条件下的加载试验,这在以往的研究中很少对SPH进行模拟。SPH/FEA方法通过模拟双轴压缩试验、浅基础承载力和颗粒介质中的轮式运动来评估。双轴压缩试验结果与单独用有限元法建立的参考解基本一致。SPH/FEA模拟得到了令人满意的浅基础承载力估计,并适当地捕捉了受分布荷载作用的边坡的土壤破坏机制。由于SPH/FEA方法可以成功地捕捉颗粒状基体与以规定速度运动的侵入体(如车轮)之间的接触或失去接触,因此,颗粒状介质中轮式运动的动态模拟比通过阻力理论(RFT)获得的速度场预测更为真实。 引言: 许多岩土工程问题涉及大变形,发展足够的计算方法来解决这些问题对工程实践至关重要。在离散元法(DEM)中,感兴趣的地质材料由颗粒元素表示。根据为保证平衡而产生的接触力,计算粒子的位移场和速度场。每个粒子都受到重力加速度、弹性接触力以及相邻相互作用粒子的耗散法向力和摩擦力的作用。DEM非常适合分析颗粒柱倒塌等小尺度土力学问题和土/固相互作用,但由于其计算成本,其在高分辨率问题中的应用受到限制。DEM模型需要大量参数,如粒径、摩擦系数和颗粒形状。尽管DEM模型对这些参数很敏感,但目前还没有系统的方法来有效地校准DEM模型。例如,复制弹塑性、欠塑性或粘弹性行为需要大量的计算工作。土壤/固体相互作用模型通过组合使用DEM和有限元法,但DEM/FEM方法的使用仍然受到校准挑战和计算成本的阻碍。 物质点法(MPM)也采用粒子元来离散域,但与DEM不同的是,物质点由一组相邻的粒子表示,这些粒子被赋予连续介质力学本构模型。然后可以求解质点处的耦合微分方程,以求解位移和应力等场变量。MPM被用于解决饱和粘土侵入或砂柱坍塌等复杂问题。虽然MPM在研究土-结构相互作用问题上取得了成功,但它也有一定的局限性。首先,在背景网格上定义场变量,背景网格的作用与有限元分析(FEA)中的网格类似。在大多数MPM软件包中,一旦模拟开始,背景网格保持不变,这对于涉及复杂几何形状和大变形的问题是一个限制。其次,MPM要求使用均匀大小的颗粒对整个土壤域进行建模。第三,已知MPM对固体力学的小变形问题产生不准确的结果。与使用纯MPM模型相比,在预计变形较小的区域使用FEM可以在某些情况下提高计算的准确性。然而,将材料点模型的网格与有限元模型的网格耦合会影响网格单元中与有限元网格接触的所有粒子的位置,这有时会产生不必要的粒子运动。 由于光滑颗粒流体力学(SPH)具有真正的无网格特性,因此当FEM与SPH耦合时不存在这种不准确性。与MPM一样,SPH也采用粒子元素,但粒子不绑定到网格,这允许动态粒子细化和粗化。SPH是一种连续体无网格数值方法,非常适合于涉及流体或颗粒介质等流动材料的大变形问题。SPH基于流体运动的拉格朗日描述,其中流体由一组根据动量平衡方程运动的粒子表示。求解这些方程需要搜索每个粒子最近的邻居。DEM在模拟单个粒子相互作用和解析详细的接触力学方面非常准确,非常适合小型到中等规模的系统;然而,它的计算成本与粒子数的比例很低,限制了它对大规模问题的适用性。研究发现,DEM和SPH对于颗粒柱崩塌和颗粒沉降等经典颗粒流动问题具有相似的精度。MPM结合了拉格朗日和欧拉方法,有利于捕获大变形和复杂的边界相互作用,但它可能受到数值问题的影响,如颗粒聚类或应力传递不准确。在Arduino (2018), Fern et al.(2019)中进一步详细讨论了MPM和SPH方法的一些特征。SPH方法作为一种完全基于拉格朗日粒子的方法,在处理自由表面流动和高度变形系统方面具有最佳性能,为连续颗粒流动提供了鲁棒的解决方案;然而,其精度可能受到核平滑伪影的限制,并且其计算成本虽然低于大规模系统的DEM,但仍然显着。效率不仅取决于计算方法,而且取决于它的实现。因此,软件(ANSYS,基于matlab的实验室开发代码,或其他)和硬件(核数,CPU vs GPU等)的选择也非常重要。在本研究中,代码利用了MATLA提供的CPU并行化。 SPH规范中采用了多种土本构模型来研究大变形地质力学问题。SPH在可压缩和近不可压缩介质中的动力学问题上显示出了显著的准确性。特别是,基于黎曼解算器的空间离散化可以避免非物理静水压力波动、沙漏现象以及与缺乏守恒、一致性、稳定性或收敛性相关的数值问题。此外,数值应力扩散方程有效地消除了SPH模拟中的虚假应力波动。由于SPH最初是为流体动力学开发的,几个研究小组用它来模拟土壤液化。例如,饱和水土壤的孔隙流体采用SPH建模,其中每个流体颗粒都受到由固体骨架位移场计算的加权阻力,其本身采用离散元法(DEM)建模。在另一种SPH方法中,用弹塑性SPH土颗粒进行模拟,将超过一定塑性应变水平的颗粒转化为服从非牛顿流变的流体状态的颗粒。Biot的孔隙力学方程采用半隐式SPH算法实现,并允许模拟边坡破坏。在这种方法中,达西的阻力被隐式地更新了,减轻了渗透率,时间增量受限。通过赋予SPH颗粒有效应力和吸力的本构行为,SPH扩展到非饱和土。还开发了一个SPH模型来模拟饱和土壤对地震波的响应,其中柔性基础和自由场边界专门用于地震分析。尽管最近基于并行化和图形处理单元(GPU)使用, SPH在计算上仍然相对昂贵。此外,在准静态条件下,SPH的性能不如FEM,因此,在加载速率相对于材料变形速率较低的问题上,SPH的吸引力不如FEM。事实上,固体力学问题的SPH精度仍然是一个正在进行的研究和争论的话题,特别是在准静态条件下。为了在固体力学中应用SPH,动量平衡方程被修改以考虑固体行为,这是由弹性、塑性或损伤的本构方程建模的。通过耦合SPH/DDA(间断变形分析),可以模拟滑坡过程中土壤(用SPH建模)与刚性岩块(用DDA建模)之间的相互作用或模拟经历刚体运动的流体和土壤体积之间的相互作用。用SPH模拟可变形固体表面或可变形固体与颗粒介质之间的界面仍然具有挑战性,这限制了SPH可以研究的土-结构相互作用问题的范围。例如,在SPH模拟中,必须将固体入侵者建模为刚性边界,这样就可以忽略与土壤相互作用的刚性固体结构的小应变变形。可以用SPH颗粒来模拟固体结构,并将纯弹性本构定律赋予固体,但小应变固体模型需要大量SPH颗粒,因此自由度较大。为了缓解这一问题,一些作者提出了将SPH方法与FEM相结合的策略,但迄今为止,这些策略的实际应用有限。SPH和FEM方法相结合,用于研究切割或爆炸载荷,以及固/流体相互作用。土的动态压实和土体的准静态拱起分别在加载边界附近采用SPH模型,在远场采用FEM模型。本文作者采用FEM与SPH相结合的方法模拟了复合锚杆侵入土体,但在最高围压下,模型与实验结果不匹配。模拟约束条件下土体与可变形固体侵入体之间的准静态相互作用仍然具有挑战性。 在此,我们提出了一种将SPH方法与FEM相结合的新方法,并在MATLAB中实现了SPH/FEA模型,以模拟在准静态条件下受到大变形的刚性可变形固体(用FEM建模)与宿主颗粒介质(用SPH建模)之间的相互作用。SPH控制方程在第2节中描述。本文提出的SPH/FEA耦合分辨率算法的原理见第3节。第4节详细介绍了SPH边界条件和初始应力场条件的实现。我们使用提出的SPH/FEA来模拟各种应力路径和地质力学中感兴趣的边值问题,例如双轴压缩问题、浅基础承载力问题和土壤上的轮式运动问题。结果将在第5节中讨论。 图表
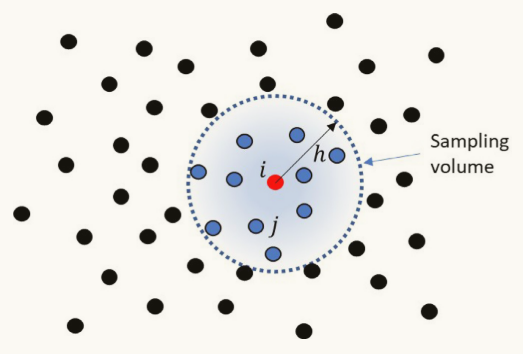
图1 SPH中使用的平滑核,通过在影响距离(或平滑半径)内采样一个邻近的聚合体
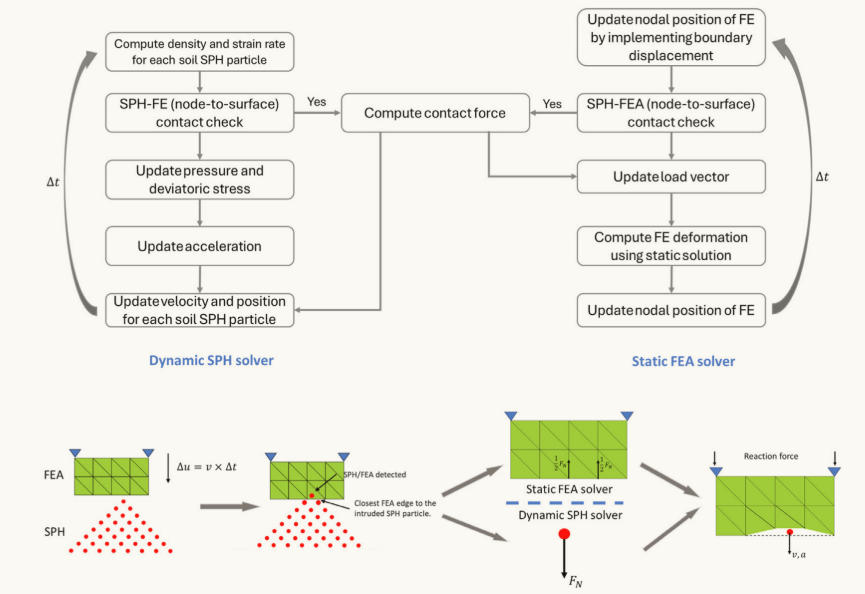
图2 该算法应用于SPH/FEA耦合方法

图3 SPH方法中的边界条件处理,在自由表面(a)和包含SPH域的固体表面(B)外附加两层或多层鬼粒子,鬼粒子被赋予与初始状态下SPH域内粒子相同的质量和空间分布,以保证初始质量密度的均匀性.
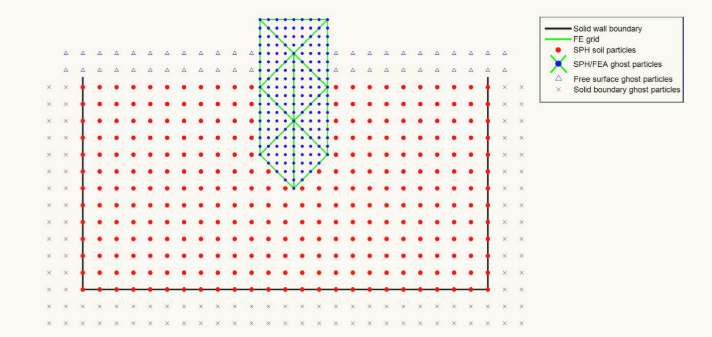
图4 SPH方法中的边界条件处理。入侵问题的例子,需要在自由表面、壁面边界和有限元域中的幽灵粒子
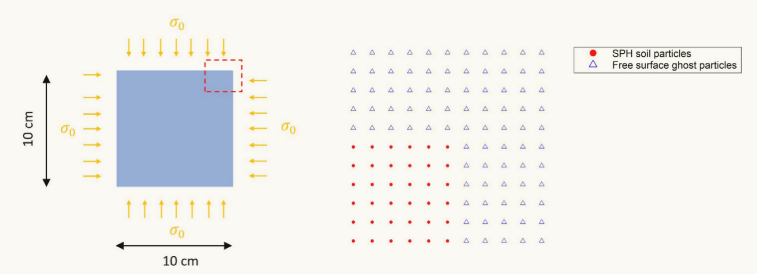
图5 各向同性约束测试。右侧的图解释了如何在左侧图中虚线所限定的区域中对域进行离散化。
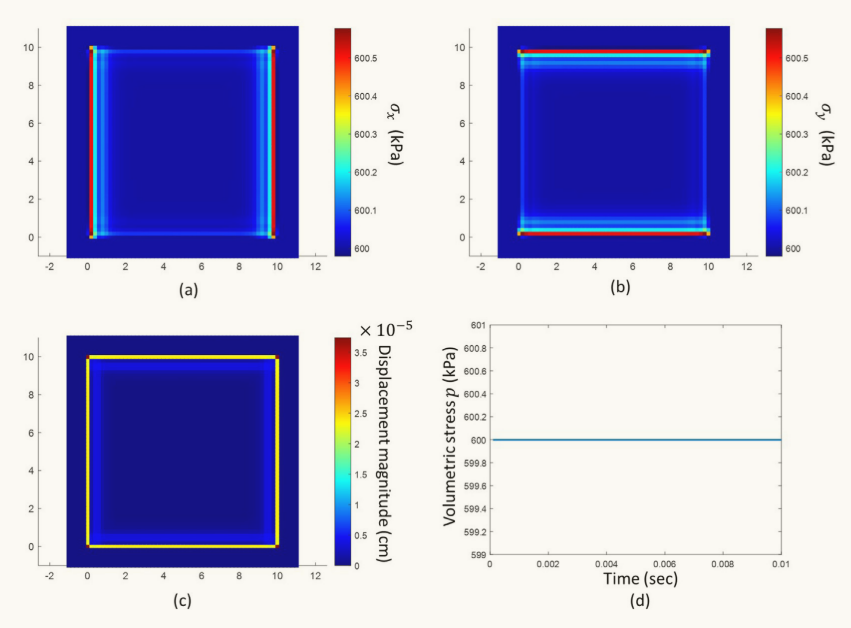
图6 各向同性约束测试的结果:(a)模拟结束时的水平应力场(0.01 s);(b)模拟结束时的垂直应力场(0.01 s);(c)模拟结束时的位移幅度(0.01 s);(d)试样中体积应力ε(也称为平均应力)的平均值。
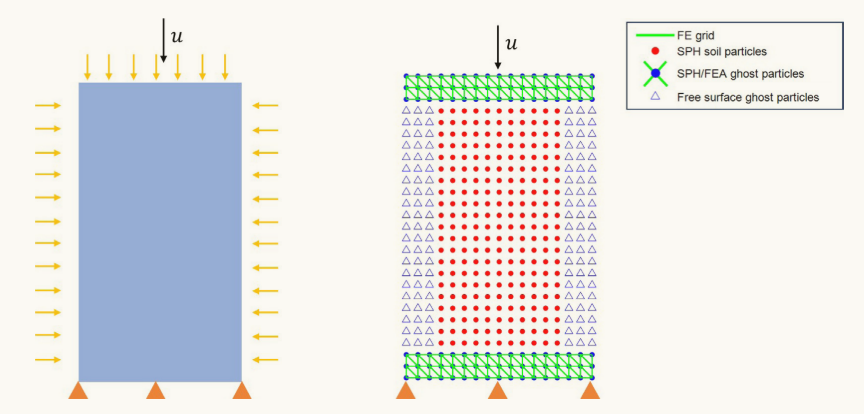
图7 双轴压缩试验的设置。左:边界条件(各向同性约束,然后单轴压缩)右:SPH/FEA模型中采用的离散化。
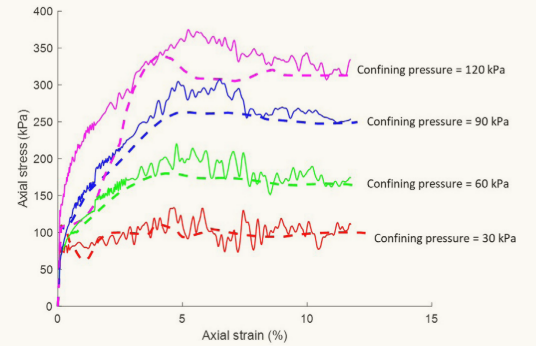
图8 通过FEM与SPH/FEA模拟双轴压缩试验获得的应力/应变曲线。虚线表示FEM结果,实线表示SPH/FEA结果。
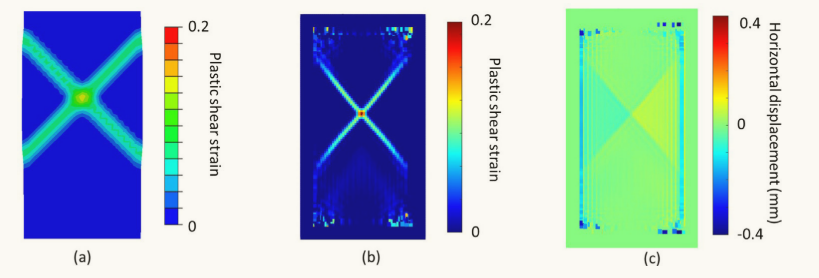
图9 在60 kPa围压下双轴应力模拟的最后阶段获得的塑性剪切应变:(a)ABAQUS FEM模拟中的塑性应变;(b)SPH/FEA模拟中的塑性应变;(c)SPH/FEA模拟中的水平位移场。
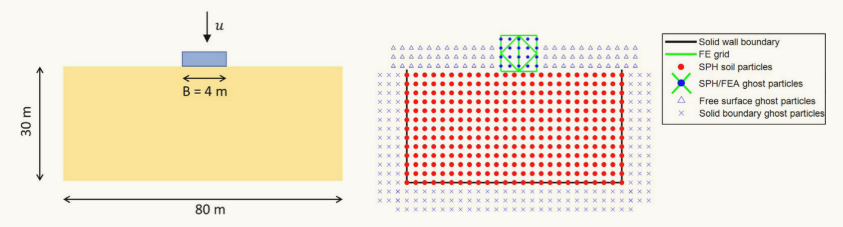
图10 浅基础模型建立
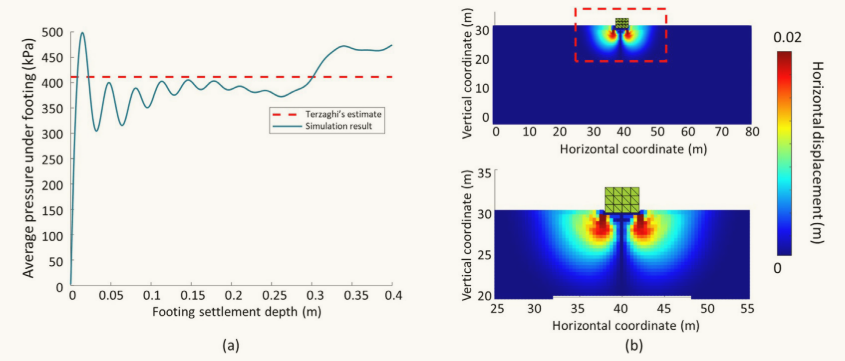
图11 用建议的SPH/FEA方法估算浅基础承载力。(a)作为施加在基础上的垂直位移函数的基础下压力的演变。(b)施加0.1 m垂直位移时SPH土壤域中水平位移场的等值线图。
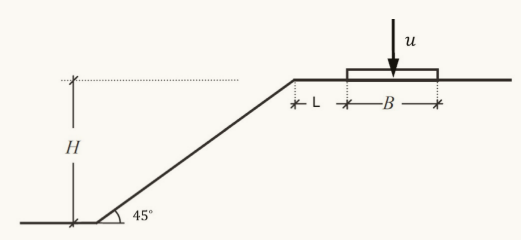
图12 坡顶浅基础问题的几何
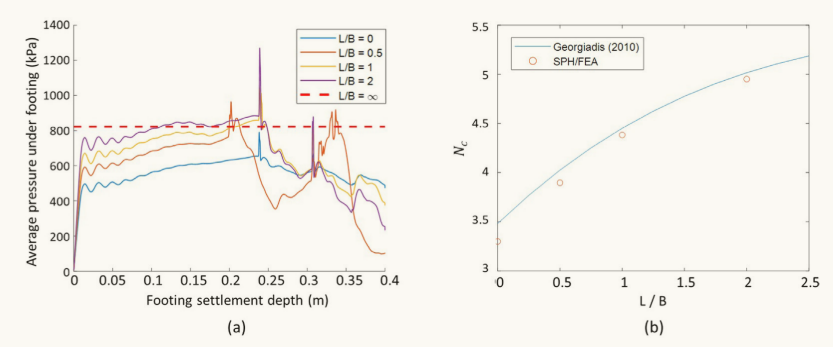
图13 位于斜坡顶部的浅基础的沉降模拟结果。(a)考虑所有后退距离比时,承载压力随外加垂直位移的演变。(b)每个后退距离比的估计承载力系数。
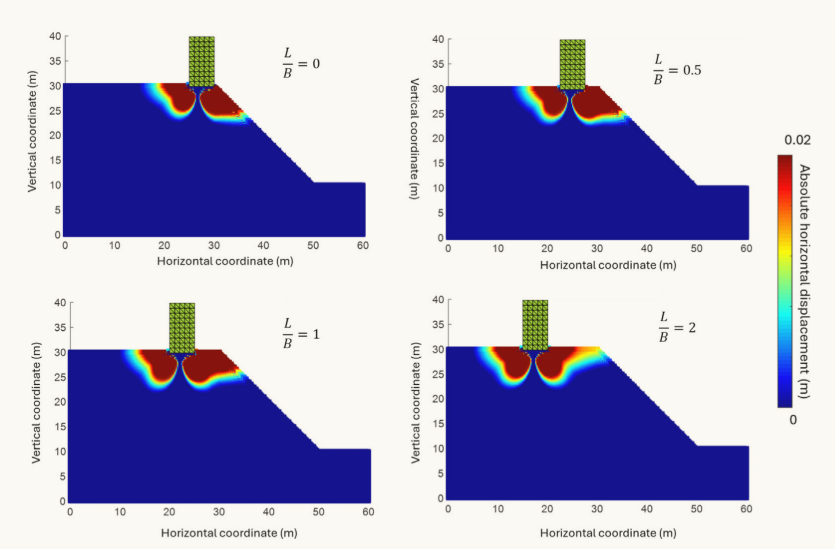
图14 坡顶浅基础地基沉降0.15m时土体的水平位移场。
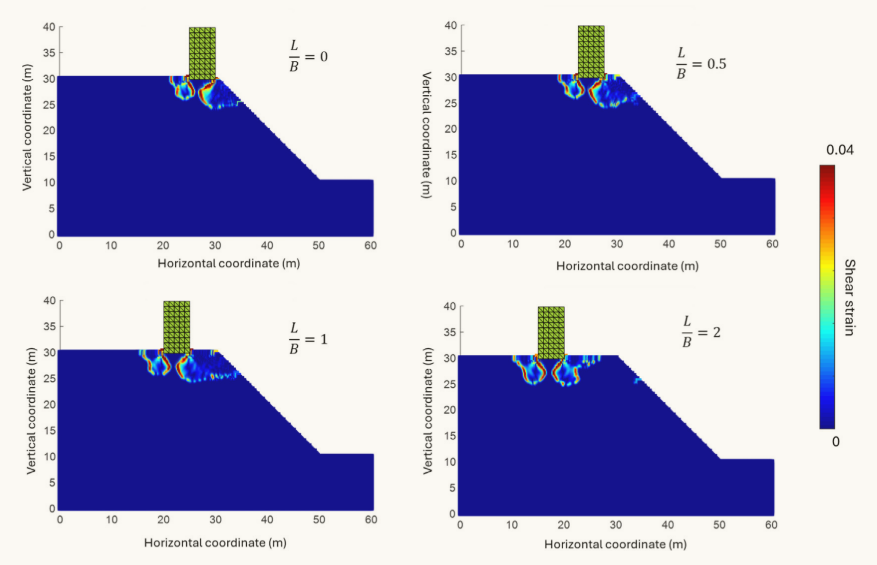
图15 坡顶浅基础地基沉降0.15m时土体的剪应变场。
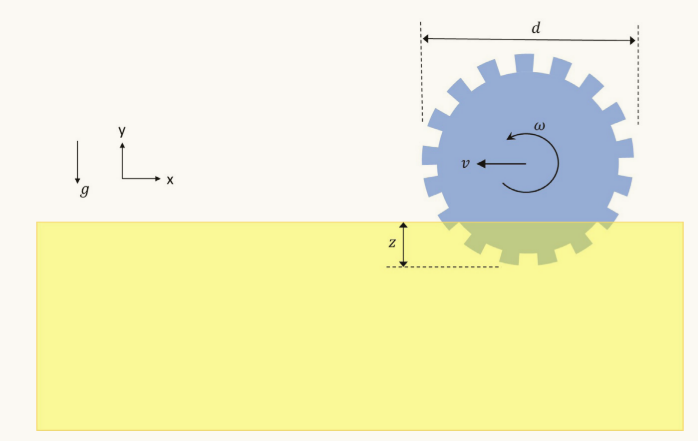
图16 吊轮运动模拟的模拟设置。
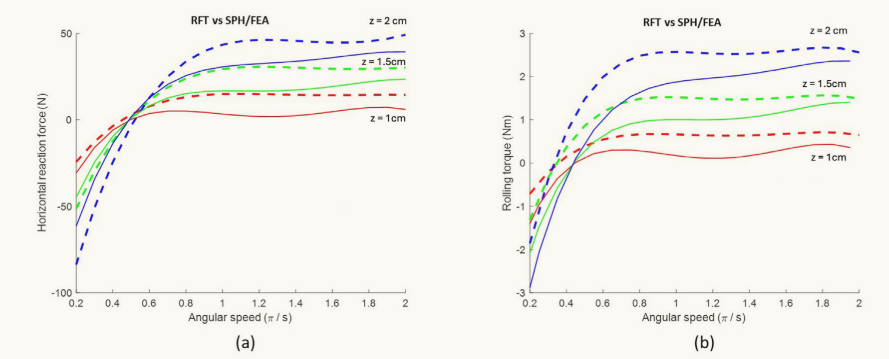
图17 车轮对5 cm/s的水平速度和不同大小的角速度以及颗粒状基底中不同的嵌入深度的反应。将SPH/FEA方法与RFT进行比较,以获得(a)水平反作用力和(b)滚动扭矩。虚线表示RFT预测,实线表示SPH/FEA结果。
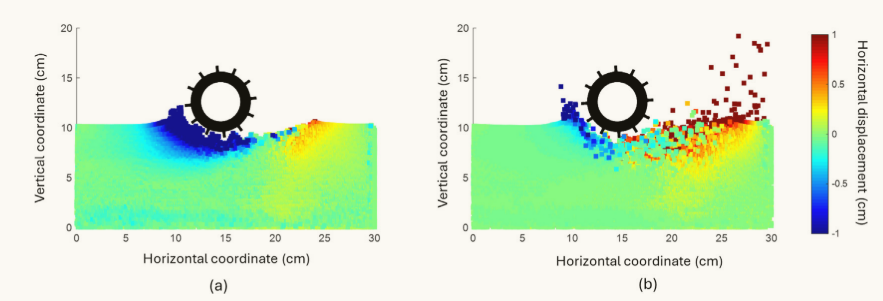
图18 埋深为1.5 cm的SPH/FEA模型的水平位移场,在(a)滑移状态下,慢自旋(0.25/ s),在(b)推进状态下,快自旋(1/s)。
结论: 提出了一种鲁棒的的MATLAB求解器,将光滑颗粒流体力学(SPH)和有限元分析(FEA)有效地结合起来,用于模拟各种类型的地质力学问题。SPH和FEA域之间的相互作用通过惩罚方法处理,即使用颗粒穿透距离来计算FE固体与颗粒接触时施加的反应。惩罚方法保证了质量守恒。 在自由表面、固体边界和SPH/FEA界面处引入鬼粒子保持了边界和界面附近的粒子采样精度。本文的另一个重要贡献是提出了在SPH/FEA模型中应用初始应力场的方法,该方法可以模拟约束条件下的加载试验,这在以往的研究中很少使用SPH进行模拟。 通过对Terzaghi承载力方程的浅基础模型进行基准测试,验证了SPH/FEA方法的有效性。该方法随后被用于模拟入侵和推进。SPH/FEA方法成功地捕捉到边坡临近时地基承载力的下降,预测的承载力系数与文献一致。SPH/FEA还允许在颗粒基板上模拟轮式运动,并捕获滑移和推进之间的转换,作为恒定施加水平速度下施加角速度的函数。我们认为SPH/FEA对土壤速度场的预测比通过阻力理论(RFT)得到的预测更真实,因为SPH/FEA可以成功地捕捉到在不同旋转速度下固体轮与颗粒基板之间的接触或失去接触。 所提出的SPH/FEA方法利用了MATLAB的并行计算工具箱。模拟在一个40核的CPU上运行。对于中等规模的问题,此设置具有可接受的性能。这种设置下的模拟时间与SPH粒子的数量近似成线性关系。这主要是因为模拟是准静态的,这避免了在每个时间步执行全邻居搜索。该策略显著降低了SPH域全邻域搜索和SPH/FEA接口入侵检测的计算量。虽然这种设置对于可以简化为2D问题的2D或3D问题有效,但完整的3D模拟将需要处理更多的粒子。通过将计算迁移到基于gpu的架构以利用其并行处理能力,可以潜在地改进该模型。尽管MATLAB通过gpuArray和一组兼容GPU的函数来支持GPU计算,但本研究开发的代码中包含了许多目前与GPU执行不兼容的自定义函数。此外,由于CPU和GPU之间的数据传输瓶颈,MATLAB中的CPU - GPU混合方法往往存在效率低下的问题。因此,扩展SPH/FEA方法可以通过以下方式来处理:(i)随着MATLAB逐渐增强其GPU对复杂数值运算的支持,未来迁移到全GPU计算;或者(ii)向外扩展到具有数百个CPU内核的高性能计算集群,这些集群可以很容易地部署到大型和复杂的问题中。 虽然本文提出的模型没有与其他SPH模型(如SPH/DEM方法)进行基准测试,但在未来的工作中这样做可能会很有趣。SPH/FEA求解器的开发和验证为其在更复杂的工程问题中的应用铺平了道路,例如开挖过程中工具/土壤相互作用的研究,锚杆安装和使用的建模以及铰接实体地下运动的模拟。值得注意的是,本研究中开发的MATLAB程序利用了并行处理和GPU加速的优势,并且可以开放获取。 参考文献
He H, Arson C. SPH/FEA method for confined and intruded granular media[J]. Computers and Geotechnics, 2025, 186: 107414.
 成功提示
成功提示
 错误提示
错误提示
 警告提示
警告提示
评论 (0)