【研究概述】

地震引起的滑坡的风险预测和灾难控制对防灾减灾具有重要的意义。河海大学Huanling Wang等研究了鲁甸地震（MW6.5）于2014年8月3日在中国云南省的鲁甸县诱导的红石岩滑坡。通过使用颗粒流代码（PFC）数值模拟方法研究了滑坡滑动过程和失稳机制。还研究了速度和位移的特征以及堆积物的特征。发现在滑坡发生滑动后7.11 s时所有颗粒的最大平均速度为23.43 m/s。最大位移与高程密切相关，滑动主体后边缘的滑动时间最长。高116.1 m、长1001.1 m的滑坡坝堆积物形态的数值结果与野外调查结果吻合较好。还进行了一系列有关参数灵敏度的数值实验，以研究放大因子和摩擦系数对堆积物特征的影响。

【研究区域概况】

2014年8月3日，云南省昭通市鲁甸县发生鲁甸地震诱发的红石岩滑坡（Mw6.5），如图1（a）和（b）所示。滑坡发生在牛栏江右侧高岩岸（图1（c） 和（d）），形成了约 1200万立方米的滑坡堆积物。堆积物堵塞了牛栏江，地震后工程设计师通过加固成为滑坡坝，如图1（d）所示。滑坡坝位于红石岩水电站进水坝下游约600 m处。大坝长约为1000 m，高120 m。滑坡坝右岸坡坍塌高度为 600 m，地震后残坡倾斜角度为70°–85°。相比之下，原来的红石岩山在地震前的坡度相对较小，为54°–61°。根据野外地质调查，地震后右岸斜坡表面背面 60 m 的区域内出现了许多拉伸和卸载裂缝。裂缝宽度和深度分别可达30 cm和 60 cm，如图2所示。

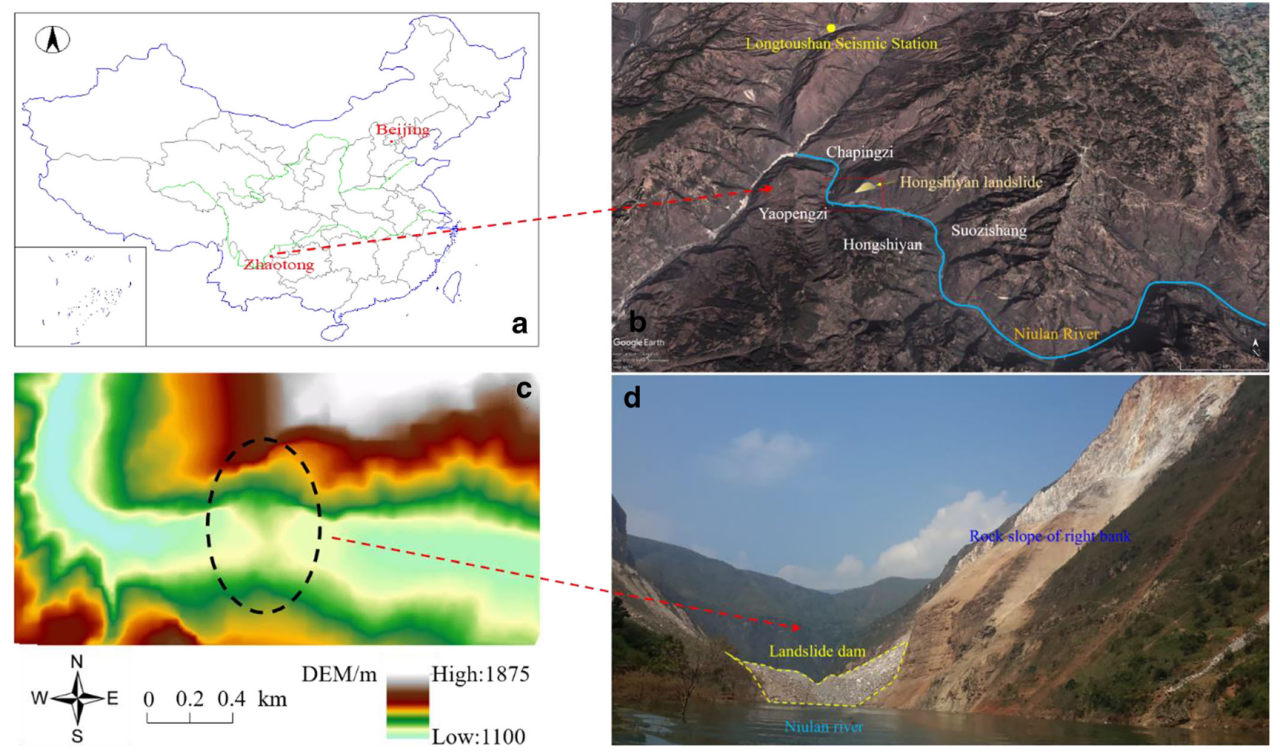
图1.（a）红石岩滑坡的位置。（b）研究区域的遥感图像（来自 Google Earth）。（c）地震后地形的 DEM 等值线。（d）滑坡坝

图2. 现场测量的裂纹宽度（a）和深度（b）

地质平面图如图3a所示。震中和前缘剪切出口的海拔分别约为1400 m 和1200 m。滑坡面垂直高度约为700 m，海拔为1100至1800 m。地震引起的滑坡运动持续时间约为120 s。滑坡路径的水平距离（从滑坡顶部至坍塌体的远端边界）约为1274 m。此外，可以看出，对岸存在着一除没有记录的古滑坡。在2014 年鲁甸地震期间，这块古滑坡稳定，起到了阻碍坍塌体运动的作用。图3b–e展示了地震后红石岩滑坡的四幅地质剖面图。根据实地调查与地质勘察结果，该区域自上而下的主要地层为二叠系（P）、泥盆系（D）和奥陶系（O）。滑坡主体主要由二叠系岩体构成，其上部为坚硬石灰岩，下部为粉质泥岩，反映出原始边坡具有“上硬下软”的结构特征。由于粉质泥岩强度较低，在上覆石灰岩的巨大压应力作用下，其变形能力较强。地震过程中，软弱的泥岩难以抵抗上覆刚性石灰岩的持续加载，导致滑坡发生。此外，相较于弱风化的石灰岩，强风化石灰岩更易发生破坏。F5断层为一条控制断层，主要由岩石与断层泥组成，大致沿滑坡方向延伸。

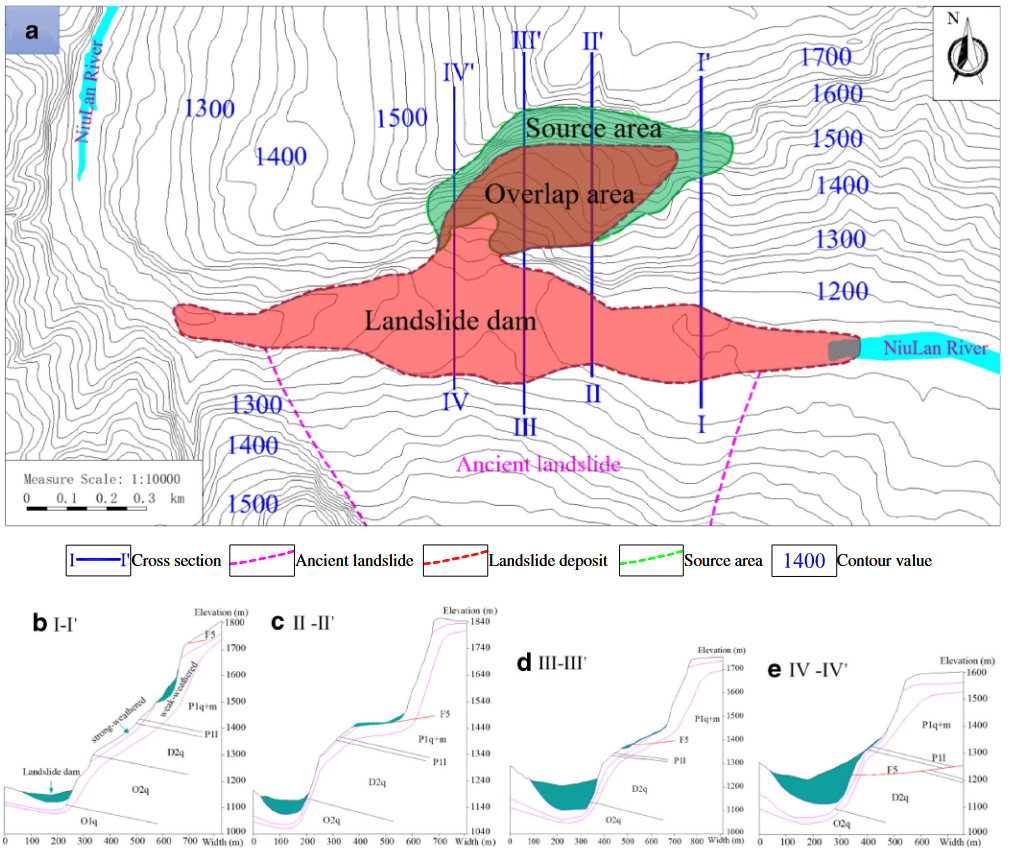
图3. a工程地质平面. b-e四种典型横截面的轮廓图

为解释红石岩滑坡地震诱发失稳的机制，研究综合考虑了滑面发育、岩体崩解以及复杂地形等因素。如图4所示，在地震动作用下，崩塌区I原始山体后缘产生张裂缝，并逐步扩展、贯通，最终形成了大尺度的张裂面。同时，由于F5断层和弱粉质泥岩层（P1l）的存在，其低抗剪强度加速了滑坡的失稳过程，导致滑面形成，崩塌区II的岩体沿滑床向自由面方向滑动。在滑动过程中，强风化岩体对周围岩块产生挤压与破碎作用。刮削区的凸起部位可见明显擦痕，对破碎岩块的运动产生阻滞作用。最终，破碎岩体沿主滑面滑动并堆积于坡脚，形成滑坡坝。

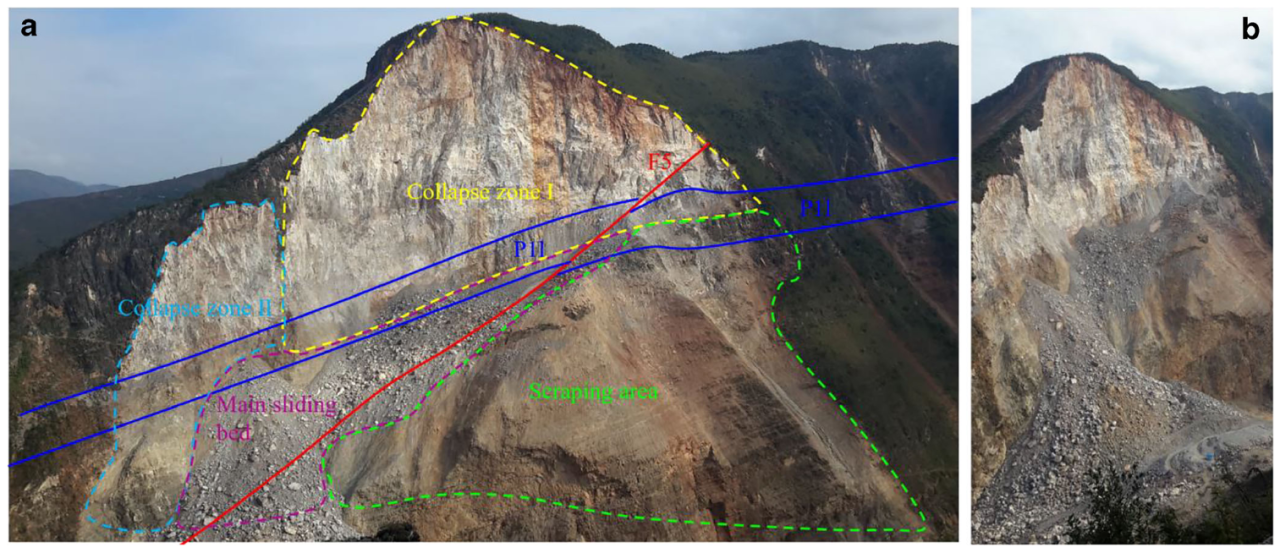
图4. 基于野外调查的红石岩滑坡崩塌过程

【数值模型和地震加载】

1.滑坡模型

本研究中采用颗粒流程序（PFC）模拟滑坡运动过程，该方法通过有限数量的颗粒与刚性边界建模，能够较好地表征岩体的不连续性与非均质特性。在PFC模型中，颗粒在模拟过程中可处于结合或分离状态。借助离散元方法，不仅可以捕捉滑坡的起始模式，还可模拟其运动路径及最终堆积形态。这些特征有助于评估滑坡灾害与减少财产损失。

基于滑坡滑动前后的数字高程数据，提取了滑面与滑体的详细数字地质信息。建模过程包括地形数据处理与几何模型构建，如图5所示。在PFC3D中，滑面与滑体分别由墙单元与颗粒单元建模（见图6）。值得注意的是，球形颗粒的总体积为1140万立方米，与实际滑体体积（1200万立方米）非常接近。这些颗粒是“嵌入”坡体内部的，而非仅放置于地形表面。在初始状态下，岩体颗粒在重力作用下不会发生滑动。

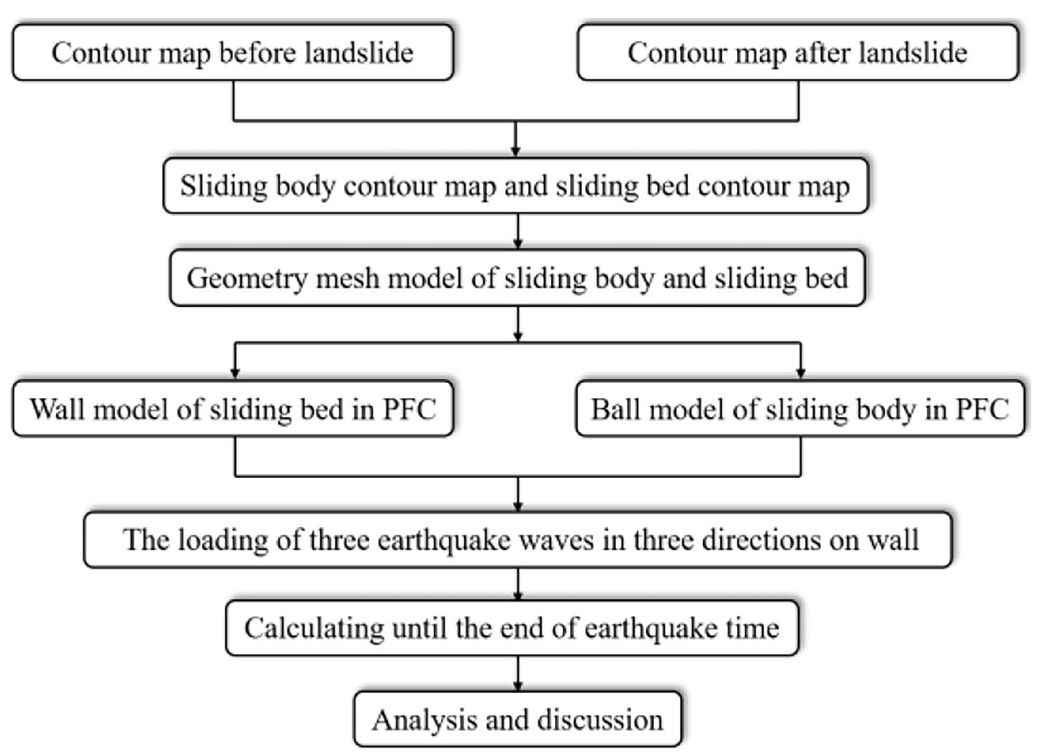
图5. 滑坡的建模流程图

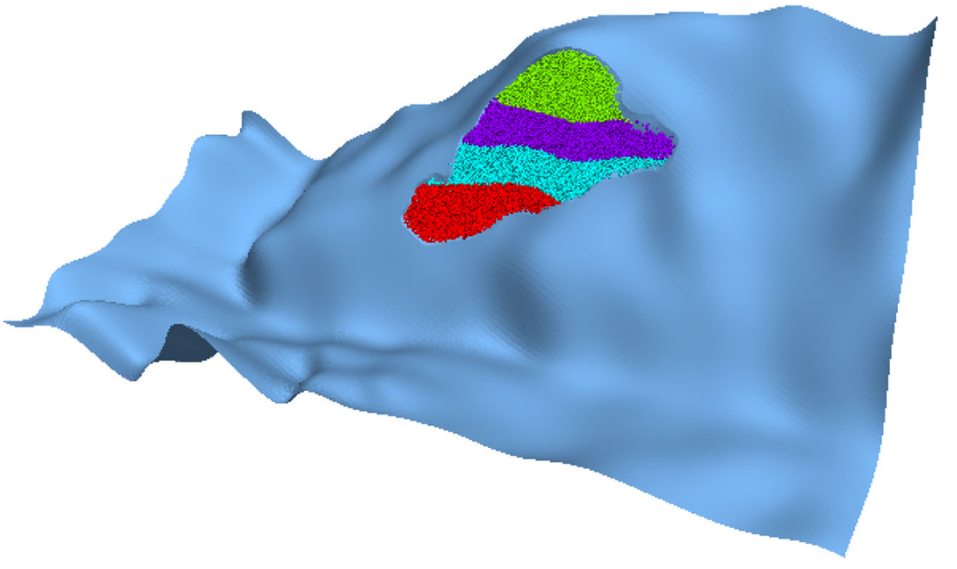
图6. 数值模型

2. 参数的校准

在三维滑坡模型中，滑面由67251个墙单元组成，滑体由30371个颗粒单元构成，其颗粒半径在2.8至4.8 m之间。需要指出的是，根据现场调查，滑坡物质的粒径范围从几毫米至数十米不等，而目前尚无有效方法能通过球形颗粒准确表达这一特征。同时，为提高计算效率，对滑坡物质的粒径分布进行了适当简化处理。

在PFC模型中，需要设定颗粒的微观参数以及接触模型参数，以模拟岩体的宏观力学特性。然而，目前尚无优于试错法的方法能有效建立PFC微观参数与实验获得的宏观参数之间的对应关系。依据现场地质调查提供的崩塌岩体参考值单轴抗压强度为70-90 MPa，杨氏模量为6.0-10.0 GPa，泊松比为0.22，开展了一系列数值实验用于参数反演与标定。在建模过程中，选取平行粘结模型（PBM）作为颗粒间的键合方式，用以反映岩体材料的特性。键合有效模量对应于杨氏模量，法向与切向刚度比与泊松比相关，平行键抗剪强度则与单轴抗压强度相关。通过一系列压缩模拟试验（如图7所示），获得了适用于本模型的颗粒微观参数与平行键参数（见表1）。此外，为了反映滑坡在动态加载过程中的能量耗散，还引入了粘性接触阻尼比。

表1 PFC滑坡模型的微观参数

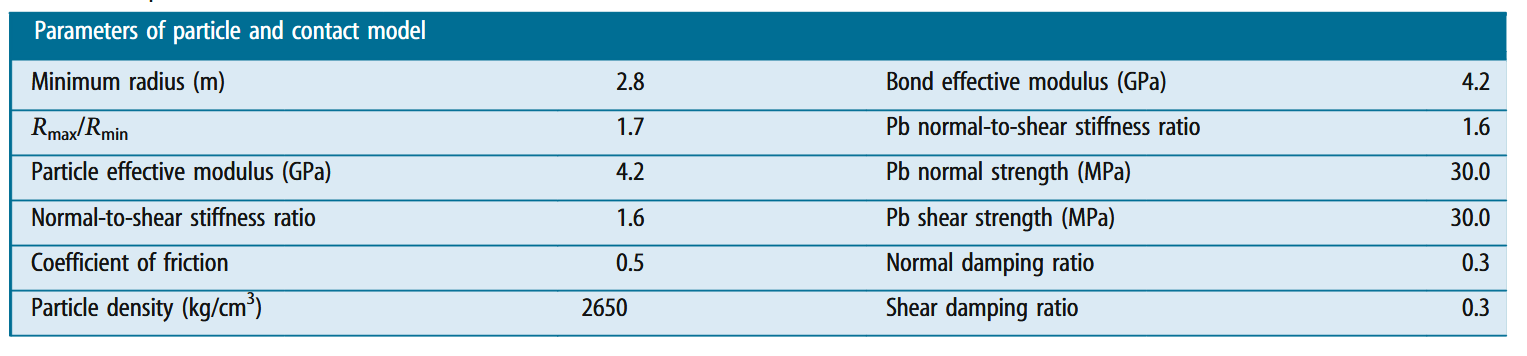
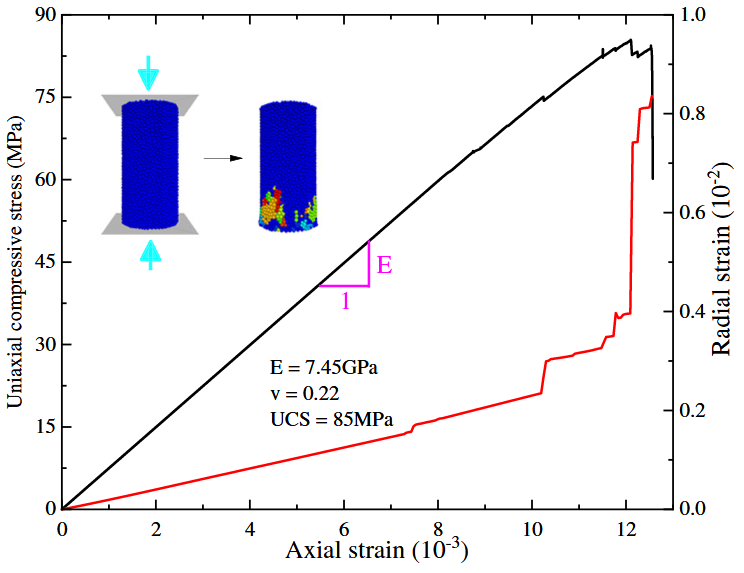
图7. 通过单轴压缩实验的微型参数的校准过程

3. 监视点设置

为探究滑坡的崩塌机制、失稳过程及运动路径，在滑体表面共布设了9个监测点，覆盖上部、中部与下部区域，如图8所示。通常情况下，速度与位移的变化能够较为真实地反映滑体的运动过程。

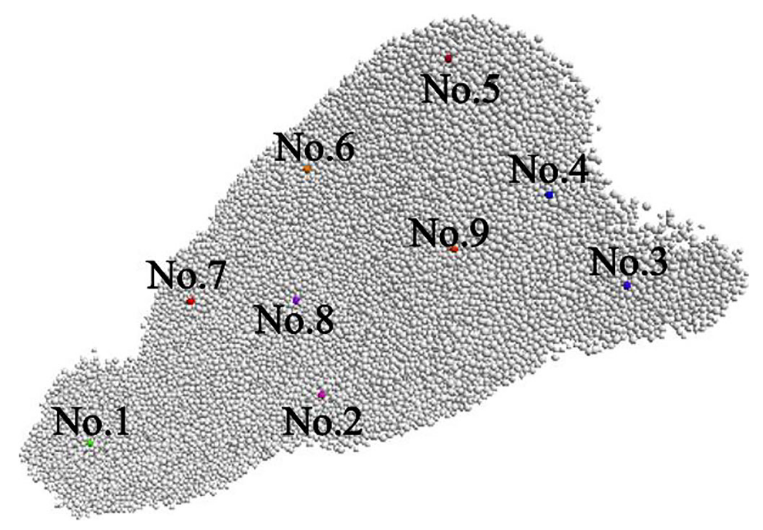
图8. 滑动体表面的监视点

4. 地震波加载

在PFC3D的动力分析中，通过对实测地震加速度记录进行积分获得三向速度时程，并将其施加于墙单元，以模拟地震振动作用。加速度时程来源于邻近的龙头山地震台站记录，如图1(b)所示。该地震记录时长为120 s，但由于其他时段的加速度值接近于零，仅选取20～40 s之间的部分（共20 s）作为输入的地震加速度时程。为保证数据质量，对加速度记录进行了带通滤波处理并进行了基线校正（见图9）。本研究在分析红石岩滑坡区域的地震响应时，考虑了地形对地震动的放大效应。根据已有研究成果，选取放大系数为2较为合理，可用于红石岩滑坡的地震动分析。

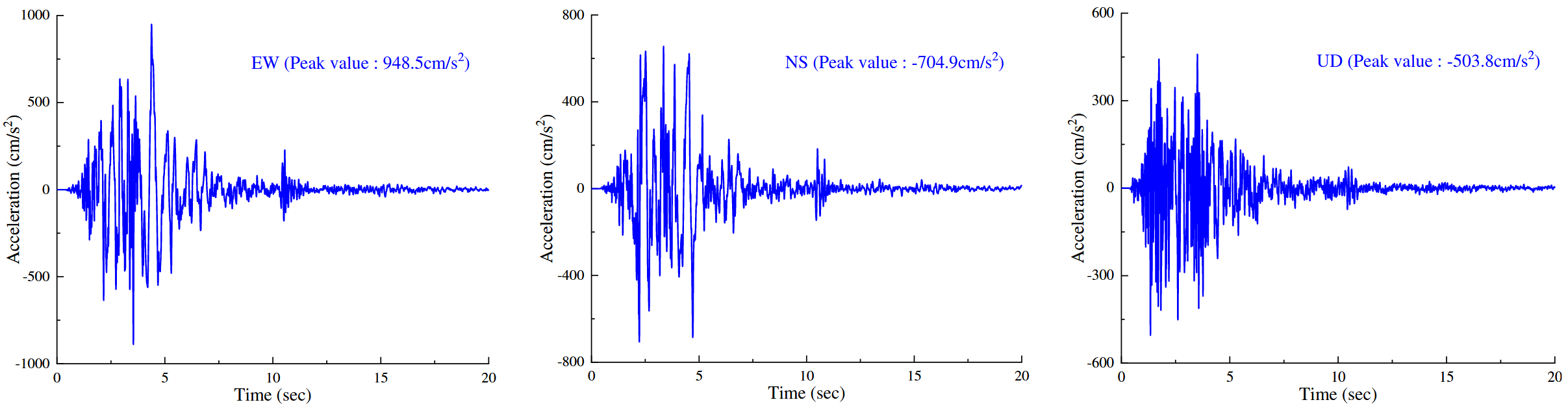
图9. 鲁甸地震的加速度分量（E-W，N-S以及垂向）

【模拟结果和讨论】

1. 速度特征

为研究地震载荷下滑坡的运动与变形特征，本文绘制了滑坡全过程的速度场分布，如图10所示。整个滑坡过程持续约120 s，其中前20 s滑体受到地震动作用，后100 s仅受重力作用。从地震时程分析可知，大部分地震能量集中在最初的10 s内释放，表明边坡在短时间内因强烈地震动而失稳。在整个运动过程中，颗粒的最大速度约为60-70 m/s。根据已有的大型滑坡研究成果，该速度范围是合理的。

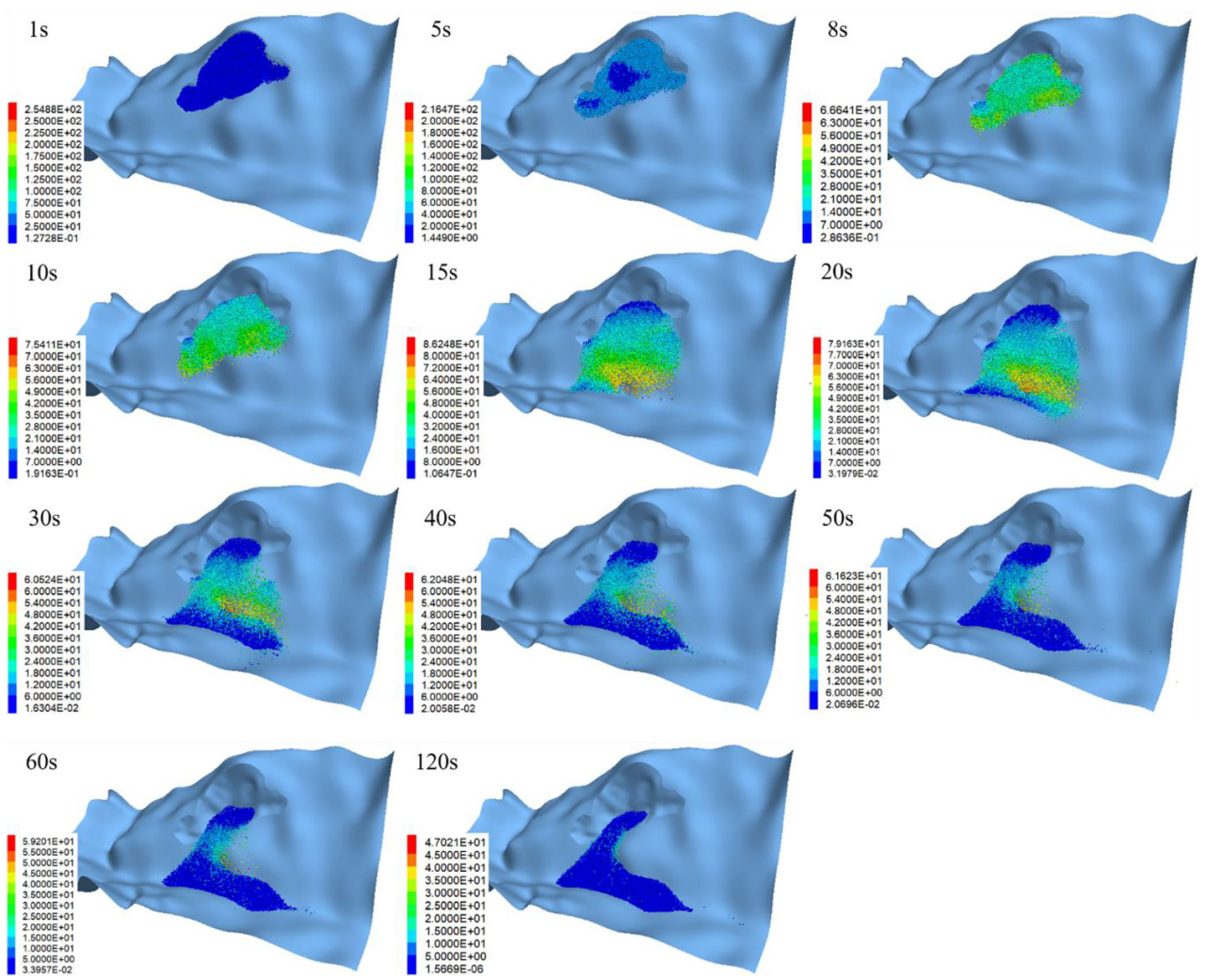
图10. 滑动过程中的速度场

如图11(a)所示，在滑坡初期，所有颗粒的平均速度迅速上升，并在约3 s时达到15 m/s。最初速度变化最显著的区域为滑坡体的前缘和后缘。上部颗粒发生相互破碎与碰撞，并推动下方岩体；同时，崩塌区II的颗粒开始沿滑面滑动。随着地震强度的减弱，速度增长速率逐渐降低，滑体最终在7.11 s时达到最大速度23.43 m/s。由于刮削区的存在，崩塌区II的滑体速度略高于其他区域。随着地震动力减弱及系统能量耗散（包括颗粒间摩擦能、碰撞能与颗粒-墙体体系变形能），滑体速度逐渐减小。随着岩块沿主滑床滑动，河谷中的滑坡堆积体高度不断增加（见图4）。当堆积体体积达到某一特定阈值（由地形条件和微观参数共同决定）时，新的稳定滑坡坝最终形成。

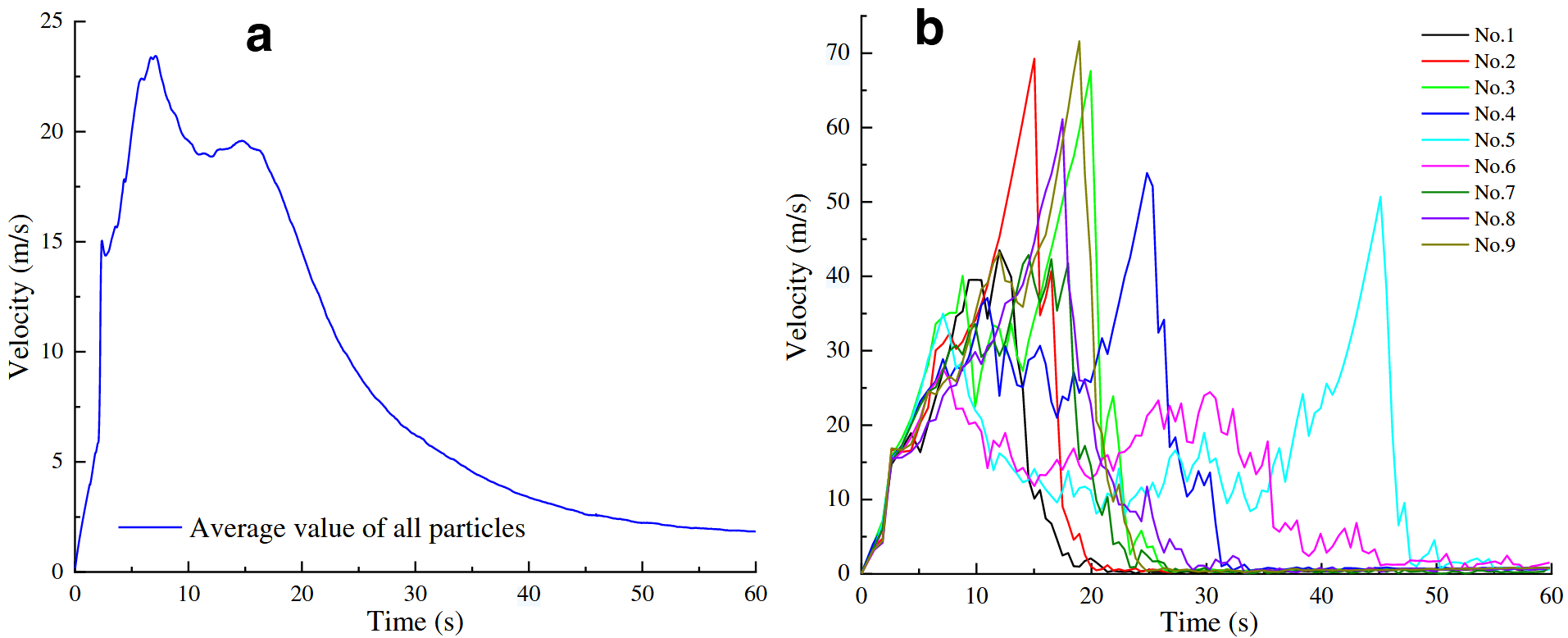
图11. a所有颗粒的平均速度，b监测点的速度

为观察滑体表面速度变化，在滑体表面布设了多个监测点。由图11(b)可见，在滑坡初始阶段，位于滑体前缘的监测点（点位1至3）速度显著上升，分别达到峰值速度39.5 m/s（点1）、69.3 m/s（点2）和67.6 m/s（点3）。值得注意的是，点3在8.8 s时速度达到约40.1 m/s后，出现先减后增的趋势（10 s至20 s之间），这主要归因于刮削区隆起地形对其运动路径的阻碍作用。对于位于滑体后缘的点5和点6，由于海拔较高且前方岩体存在阻挡，其速度峰值出现时间相对较晚。点6的速度幅值变化不大，主要受能量耗散影响。点5的速度在45.1 s时达到最大值50.1 m/s，但此时地震影响已基本消失，重力成为主要的驱动力。对于滑体中部的监测点（点4、7、8和9），其峰值速度集中出现在15-25 s之间，平均速度为53.17 m/s，基本与前缘区域速度相当。当岩块撞击对岸山体并与其他岩块发生碰撞时会发破碎，速度急剧下降。整个滑坡滑动过程中，滑体受到地震载荷与重力的共同影响，呈现出“起动-加速-减速-再加速-再减速-停止”的典型运动特征。

2. 位移特征

滑体的位移特征与其运动过程及堆积形态密切相关。如图12(a)所示，整个滑体的平均最大位移为487 m，这主要受地形限制与滑体初始高程的影响。滑体的加速阶段主要集中在0至30 s之间。对于九个监测点（点1至点9），可以明显看出，滑体前缘区域启动较早，但其运动持续时间较短。其中，前缘的点3具有最大的运动距离，为682 m，超过同区域的其他两个点。滑体后缘的点5和点6虽然与前缘几乎同时开始运动，但其位移持续时间更长，甚至在60 s时仍未停止，说明这些位置代表的岩块沿滑坡堰塞体两侧继续滚动。监测到的最大运动距离达到795 m，超过了滑体上缘至河床之间的直线距离，反映出部分岩块在堆积体形成后仍存在惯性滚动和滑移的现象。

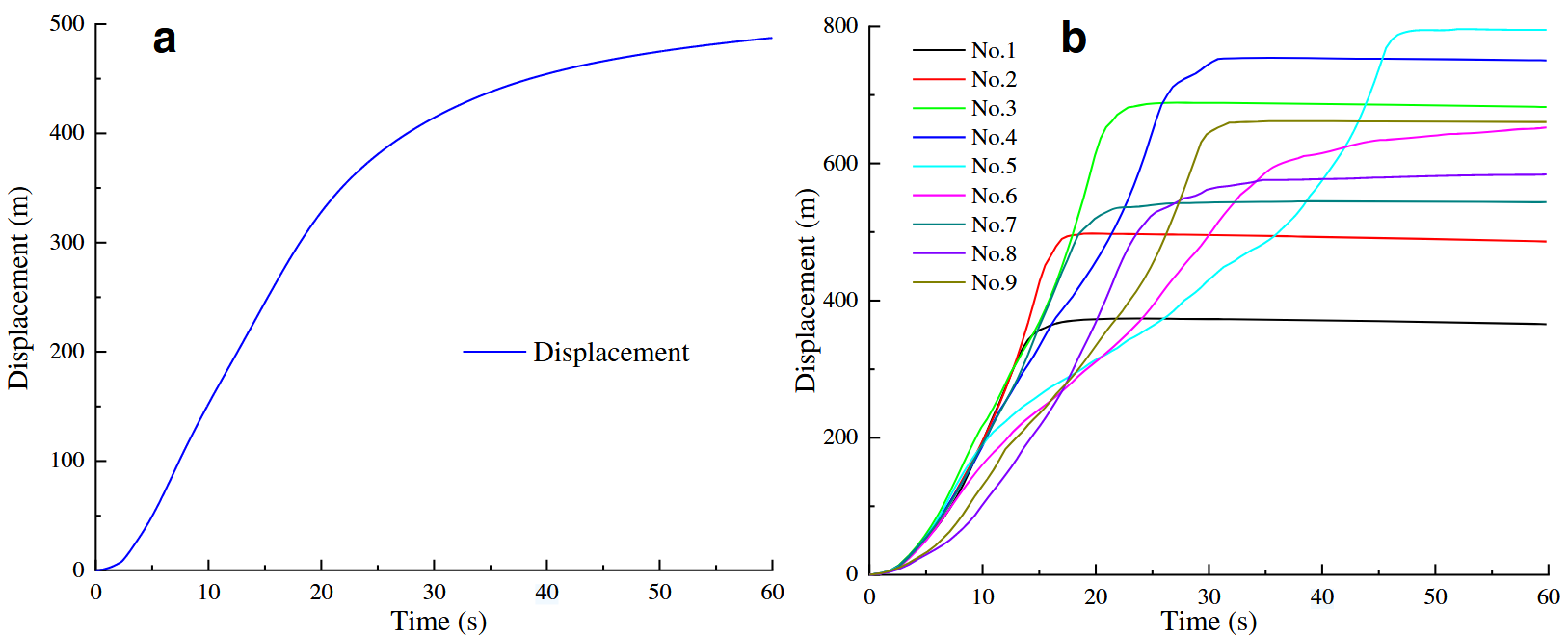
图12. a所有颗粒的平均位移，b监测点的平均位移

3. 滑坡堆积特征

为分析滑坡堆积体的特征，如破碎岩块的粒径分布及不同高程岩块的运动路径，本文记录了堆积体演化过程的一系列图像，如图13所示。图中，红色代表滑体前缘岩块（高程1200–1400 m），浅蓝色表示中部区域I（1400–1500 m），紫色代表中部区域II（1500–1600 m），绿色为后缘区域（1600–1750 m）。滑体前缘的岩块最先发生滑动，并沿河流上游方向在滑坡坝前部堆积。20 s后，岩块之间发生剧烈碰撞，破碎岩块沿前部堆积体的上下游方向滚动分布。观察发现，堆积体中并不存在明显的分层现象，不同来源的岩块在空间上相互掺杂分布。然而，结合数值模拟结果与现场调查数据可知，滑坡坝内部的核心岩块主要来源于滑体的前缘及中部区域。这些岩块在堆积体中起到了骨架支撑作用，对滑坡坝的稳定性具有关键影响。

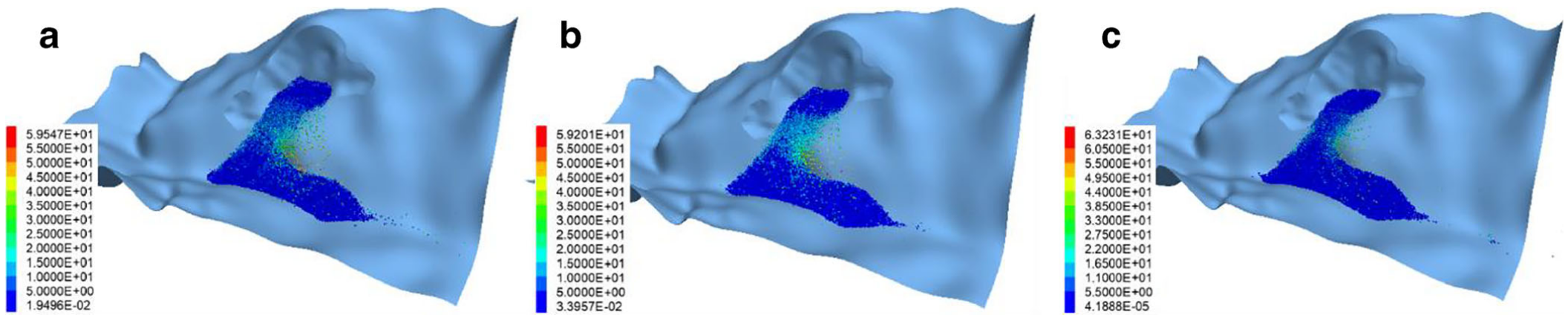
图13. 堆积演变的过程

为验证数值模拟的正确性与精度，选取了7条剖面线进行比对，包括4条垂向剖面、2条横向剖面以及1条沿河流方向的剖面，如图14(a)所示。这些剖面与震后实地监测的堆积体形态进行了对比。结果表明，尽管模型存在一定简化以及地质调查中可能存在误差，但剖面I-I′至IV-IV′仍能较好地反映实际堆积体形态。其中，堆积体从河床底部至顶部的最大高度为114.8 m。V-V′剖面的模拟结果显示堆积体高度为116.6 m，长度为1001.1 m，与实测的滑坡坝高度120.0 m、长度1000.0 m高度吻合。沿垂直于河流方向的剖面显示，滑坡坝的宽度受限于V形谷地的宽度，约为300 m。需要指出的是，若忽略滑坡形成的堰塞湖对地形的影响，滑坡堆积体下游坡面比上游坡面更陡峭，这与实际地貌特征一致。

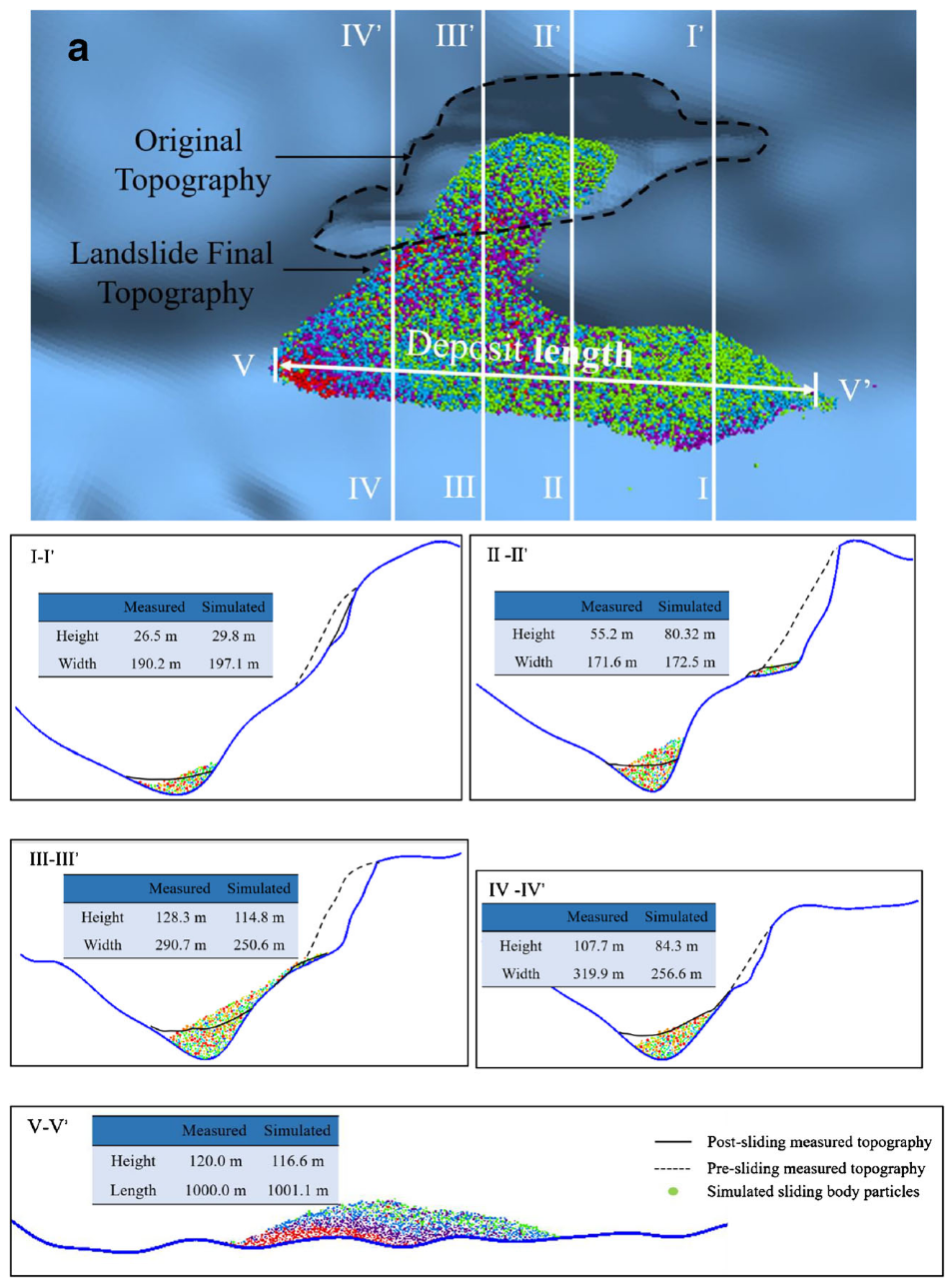
图14. 滑坡坝的堆积形态概况

【讨论】

（1）地震放大系数的影响

通常情况下，当地震波传播至地表时，由于地形复杂、高陡坡度及狭窄峡谷的存在，地震动会产生显著的放大效应。在本节中，为简化分析，忽略了因高程变化引起的放大效应差异，采用一组特定的地震动放大系数（1.0、2.0 和 3.0）对地震激励幅值进行增强。平行键断裂百分比可用于反映颗粒间键合的破坏状态，进而评估外部因素的影响，如图15所示。结果表明，不同放大系数对平行键断裂比例的影响较小。然而，如图16所示，放大系数对速度的影响更为显著，表现为峰值速度的大小及其出现时间的不同。当放大系数为2.0和3.0时，峰值速度分别为23.43 m/s（出现在7.11 s）和32.03 m/s（出现在7.14 s），这归因于前10 s内更强的地震振动。而放大系数为1.0时，峰值速度出现时间较晚。地震动放大系数在堆积体形态上的影响如图17所示。图中对比了60 s时刻（非最终静止状态）滑坡堆积体的几何形态。结果表明，地震动越强，形成的滑坡坝越长越宽越高，对下游安全性构成更大威胁。因此，在边坡工程的设计与施工中，合理考虑地震动放大效应具有重要意义。

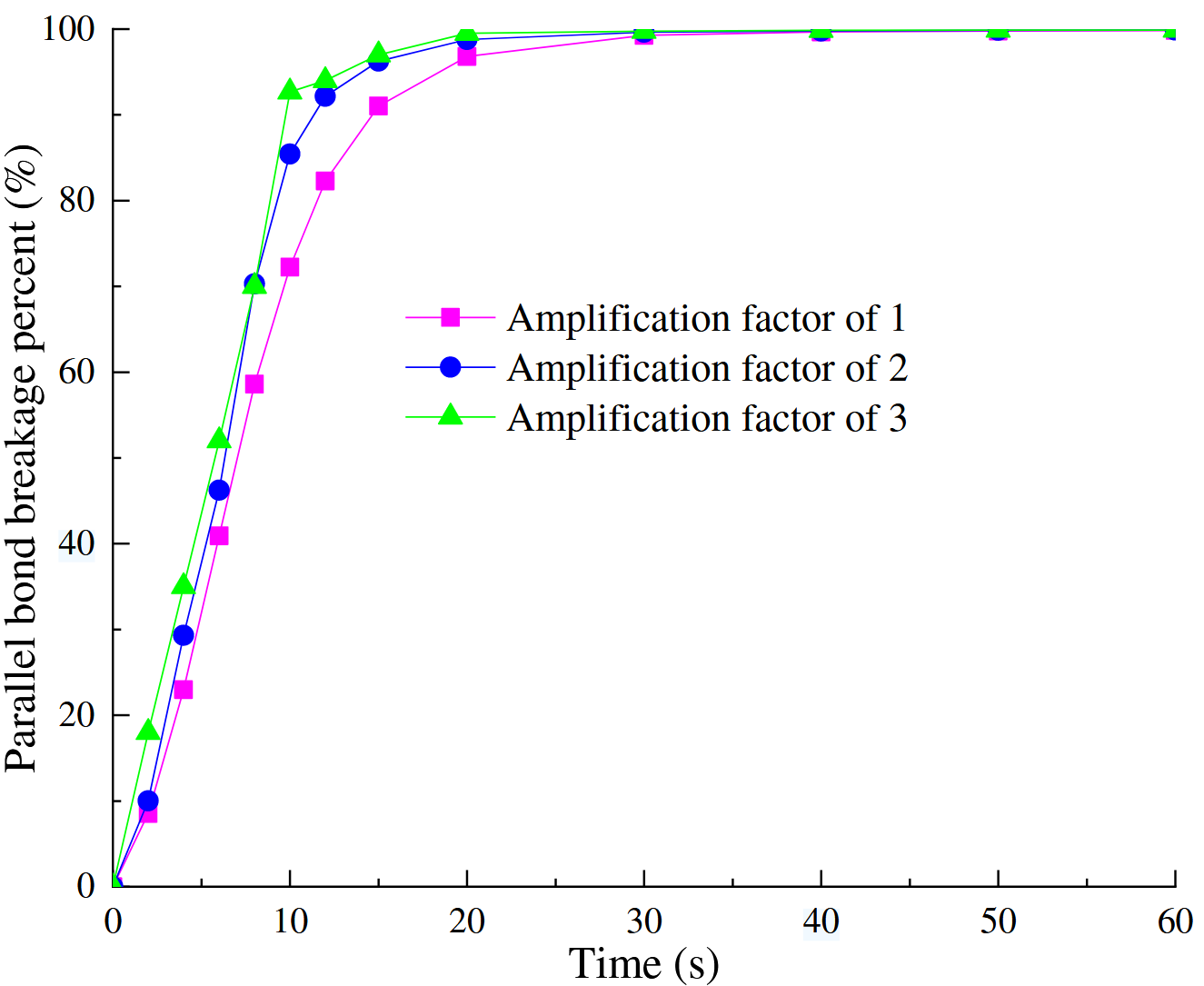
图15. 不同放大因子的平行键断裂百分比

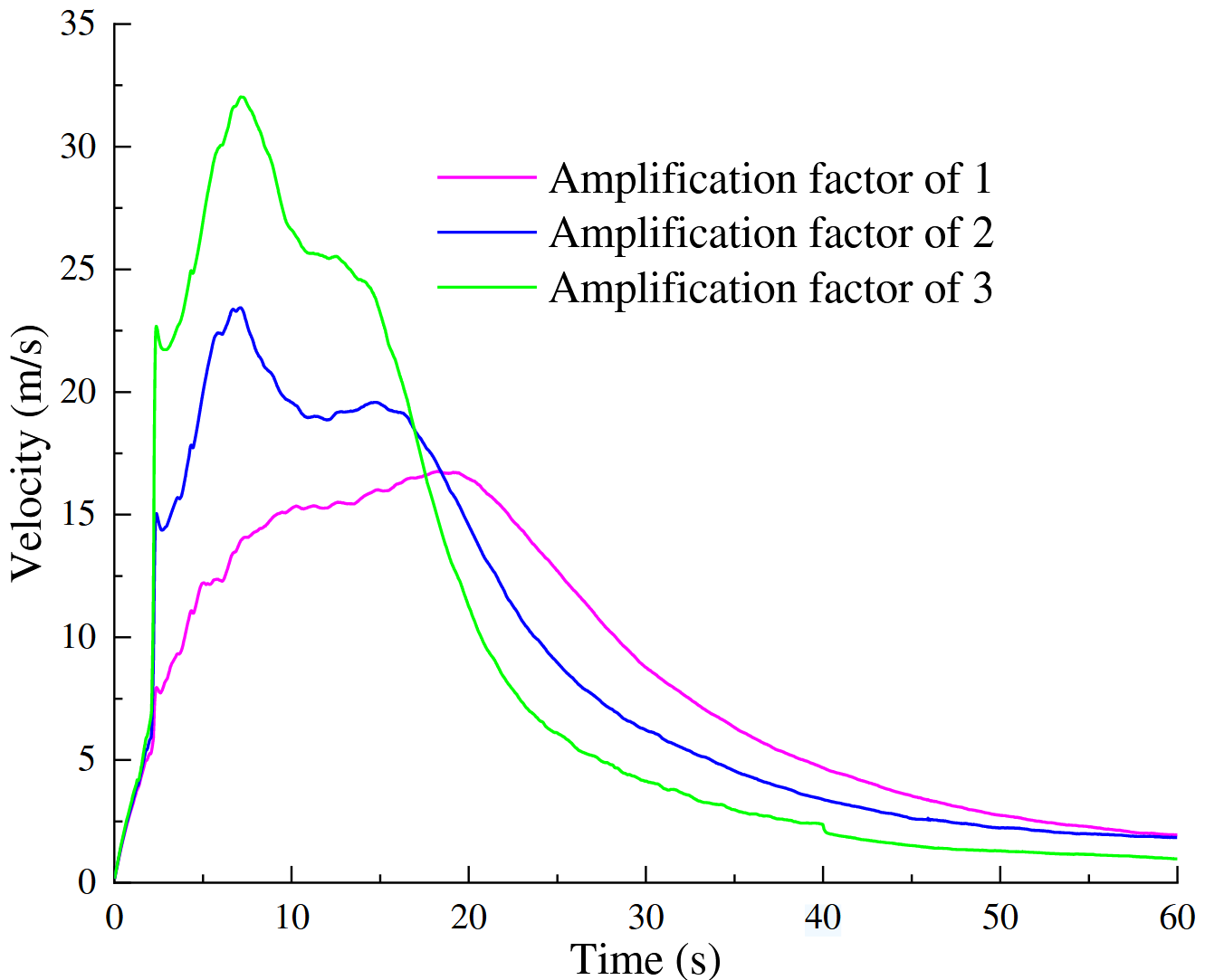
图16. 不同放大因子的所有颗粒的平均速度

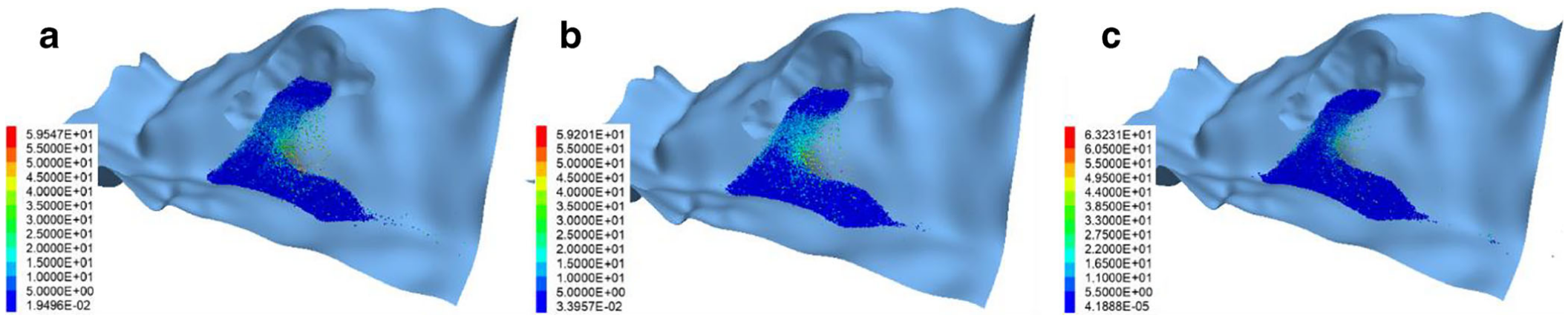
图17. 滑坡堆积体形态随地震动放大系数的变化. a放大系数为1.0，b放大系数为2.0，c放大系数为3.0

（2）摩擦系数的影响

摩擦系数是表征颗粒间摩擦及颗粒与墙体之间摩擦能量耗散的重要参数。本节中，地震动放大系数固定为2.0，摩擦系数分别设定为0.1、0.5 和 0.9。如图18所示，摩擦系数对滑体速度的影响较小，无论在速度时程的形状还是峰值上均无明显变化。这表明滑体速度主要受地震动放大系数控制，与上节讨论结果一致。然而，三种不同摩擦系数对应的滑坡堆积体形态差异显著，如图19所示。随着摩擦系数的增加，滑面上残留颗粒的数量逐渐增多；反之，摩擦系数减小时，残留堆积体的整体形态变得更长、更高。这表明摩擦系数对堆积物的分布与空间结构具有显著调控作用。因此，在滑坡灾害预测与边坡稳定性分析中，摩擦系数虽对滑动速度影响有限，但对最终堆积形态具有关键影响，需予以充分重视。

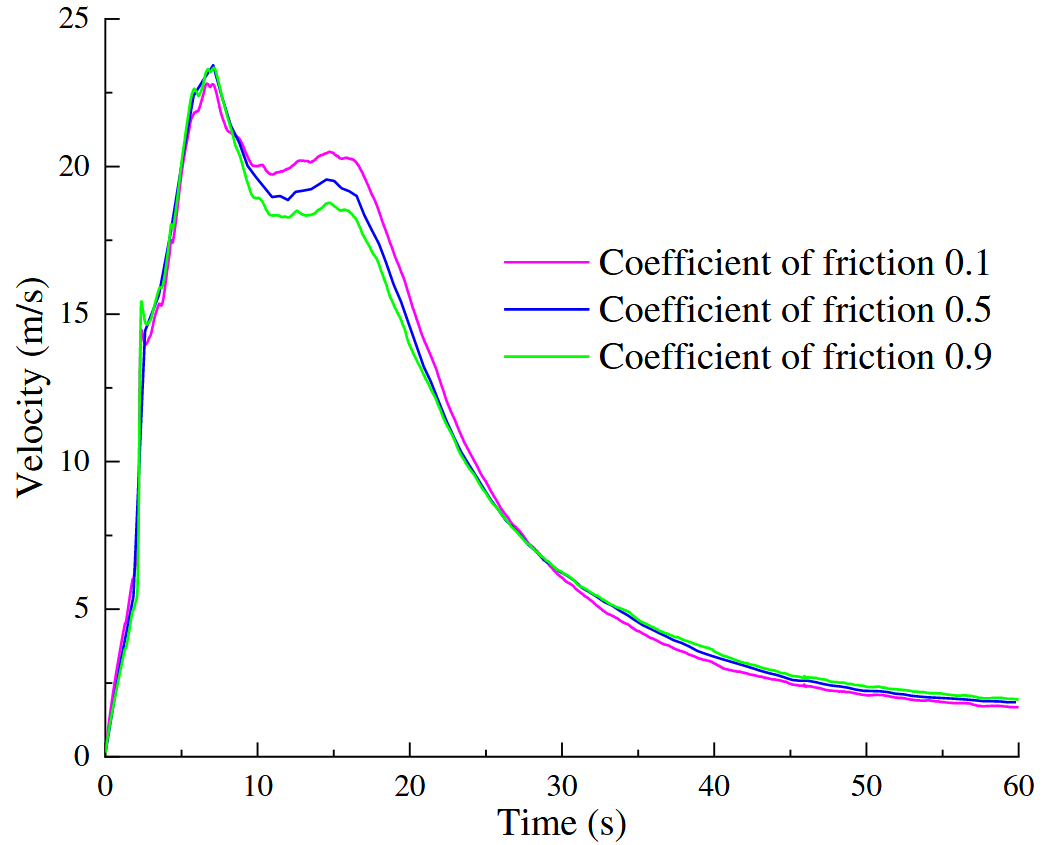
图18. 不同摩擦系数的所有颗粒的平均速度

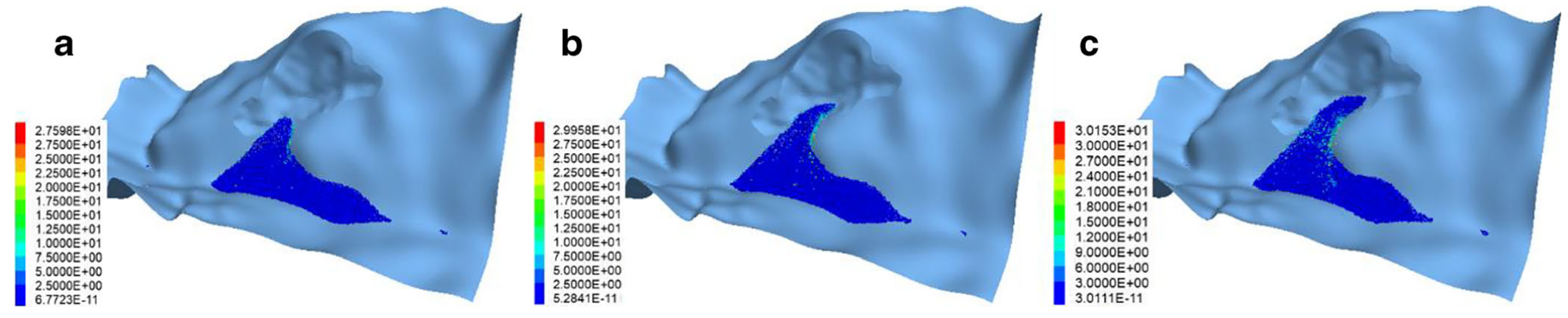
图19. 不同摩擦系数a 0.1，b 0.5和c 0.9的堆积形态

【结论】

基于地质背景、现场调查以及红石岩滑坡地震诱发崩塌的动态过程，本文采用PFC3D开展了数值模拟研究，包括微观参数的标定与物理模型的构建，以深入分析滑坡运动特征与堆积形态。研究获得以下几个重要结论。

（1）在滑坡的初始阶段，滑体的前缘与后缘最先沿滑面发生滑动；崩塌区II的滑体即将启动，而崩塌区I的后缘岩体则对下部岩块形成推动作用。所有颗粒的平均速度在约7.11 s时达到最大值23.43 m/s。滑坡前缘岩块的速度普遍高于中部和后部岩块，不同区域达到最大速度的时间也存在差异，反映出滑体在滑动过程中的非同步性和复杂性。

（2）滑体的位移特征与其初始高程密切相关。滑体后缘由于位于较高位置，具备更大的势能，在地震和重力共同作用下获得更长的滑动路径，其最大位移达795.0 m，为整个滑体中滑动距离最长的部分。

（3）数值模拟所得滑坡堰塞体的堆积形态与现场调查结果基本一致，最终堆积体的高度为116.1 m，长度为1001.1 m，较好地反映了实际滑坡规模。然而，在坡度比方面，模拟结果与实测值存在一定差异，这可能源于地形简化、模型边界条件设定或材料参数近似等因素所造成的偏差。

（4）探讨了地震动放大系数与摩擦系数对滑坡过程的影响。平行键破坏率与堆积体形态被选作评估参数敏感性的两个关键指标。

（5）研究结果表明，离散元方法（Discrete Element Method, DEM）是一种有效的工具，能够用于深入分析颗粒的运动行为、滑动过程及堆积特征。该方法能够较真实地反映岩体在地震等外部荷载作用下的非连续性、破裂演化与动力响应过程，为复杂滑坡灾害的模拟与预测提供了可靠手段与理论支持。