2025-07-02 4199 0

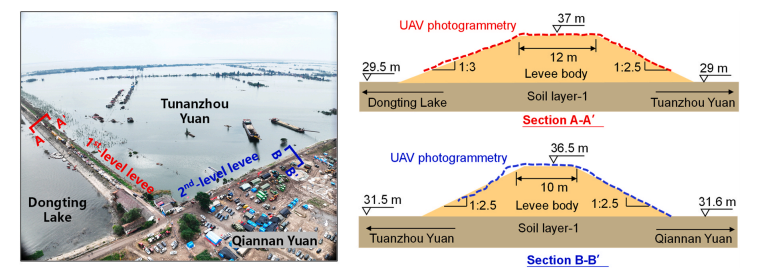
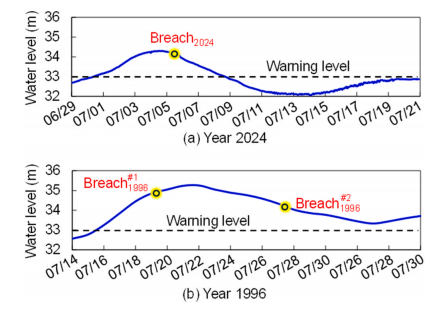
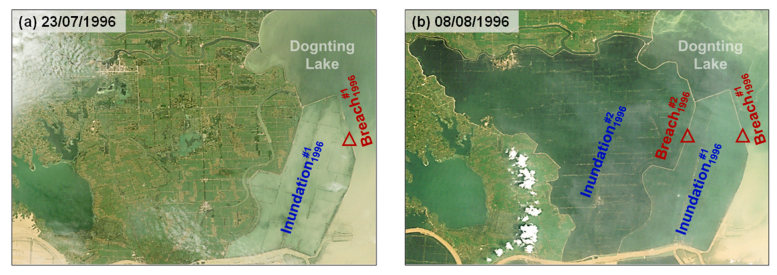
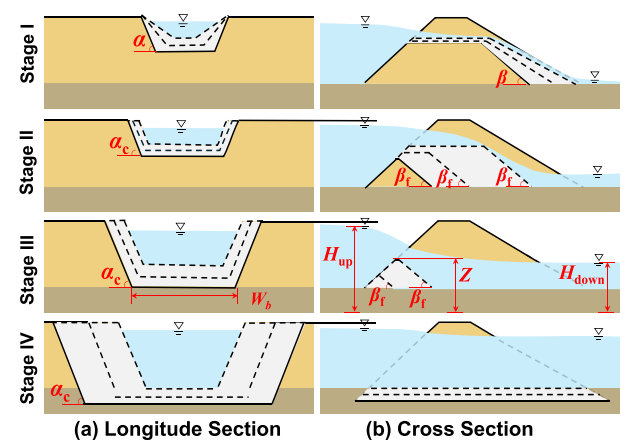
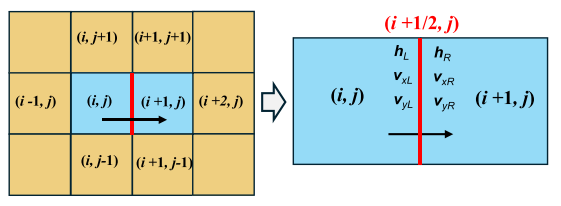
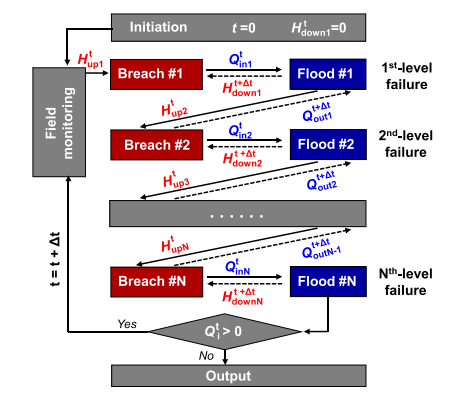
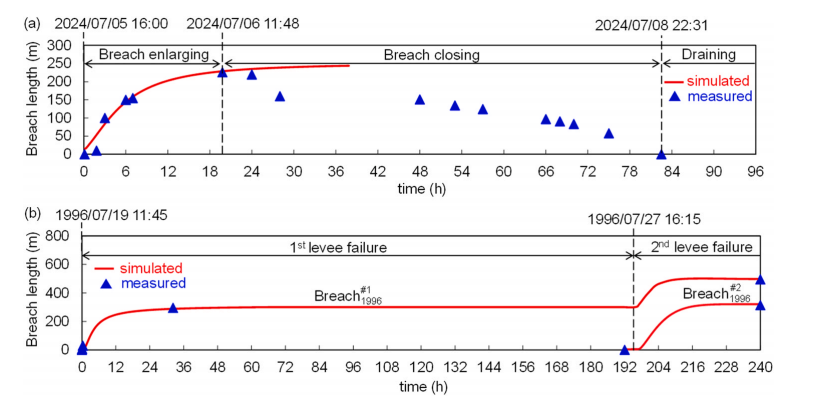
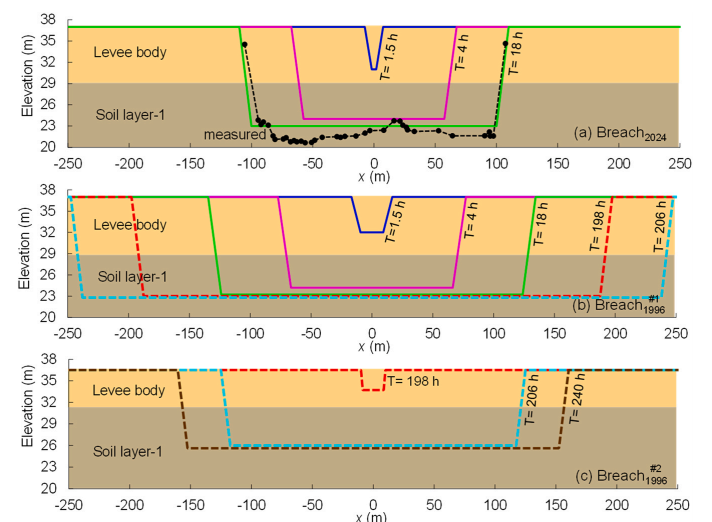
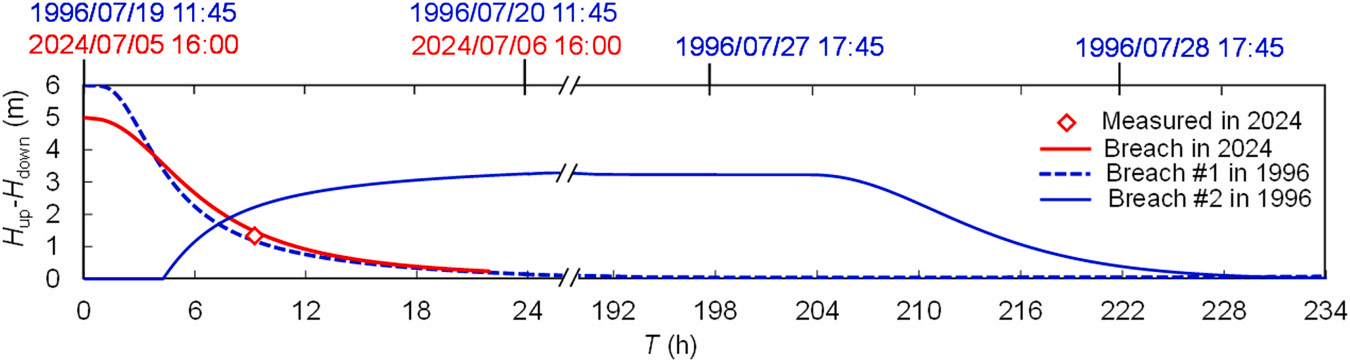
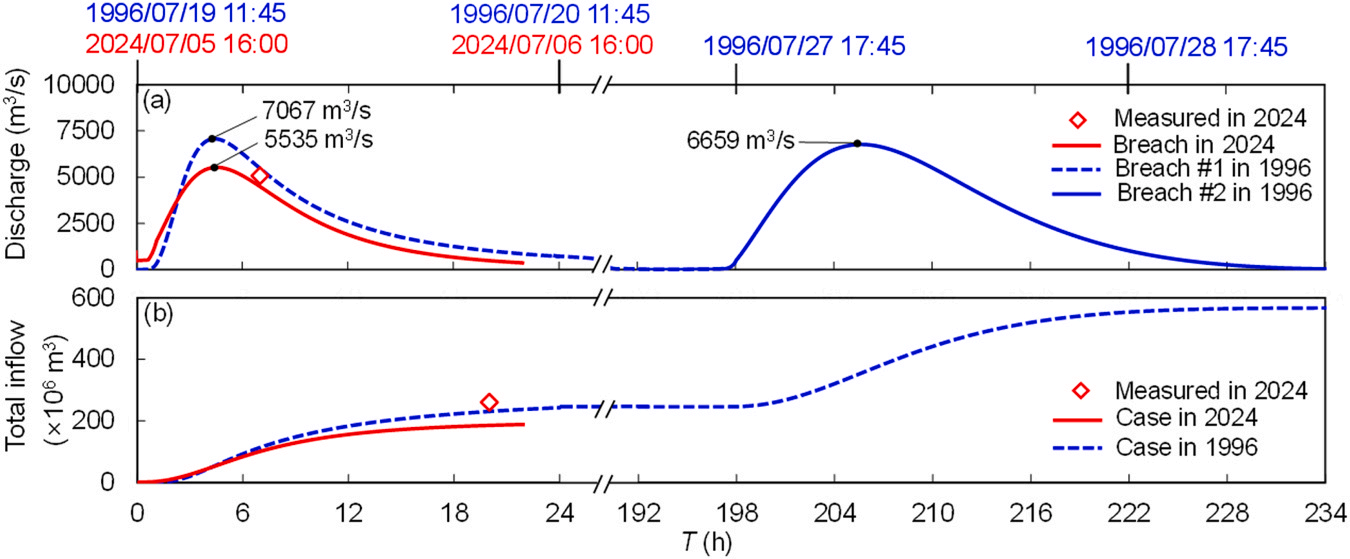
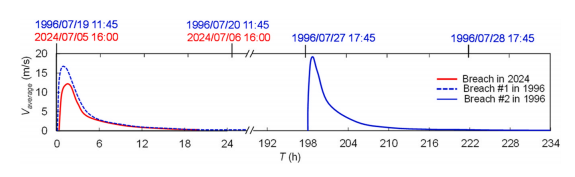
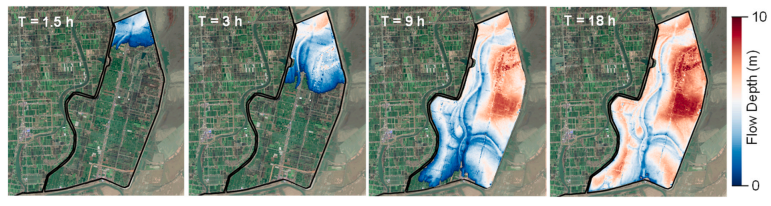
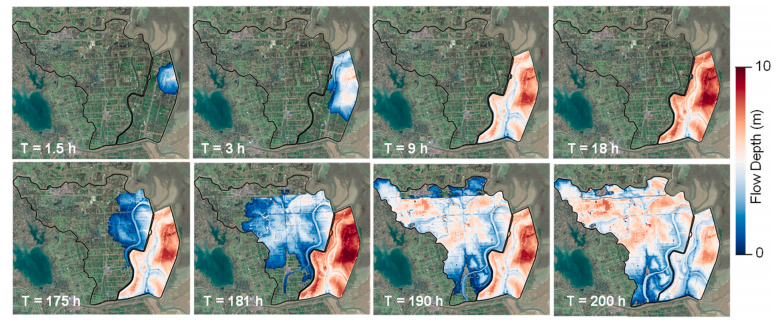
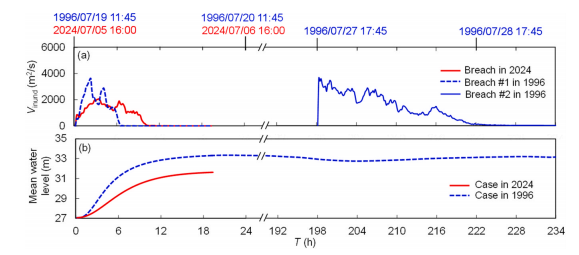
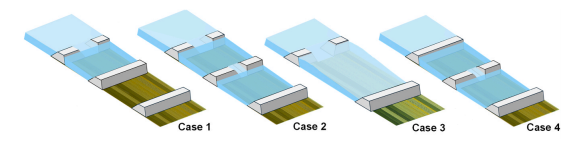
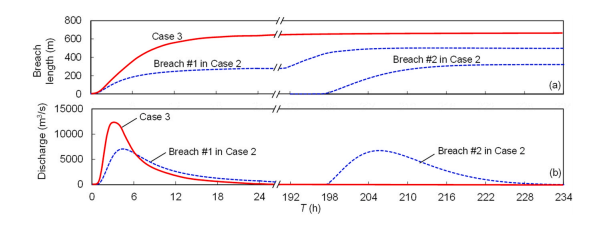
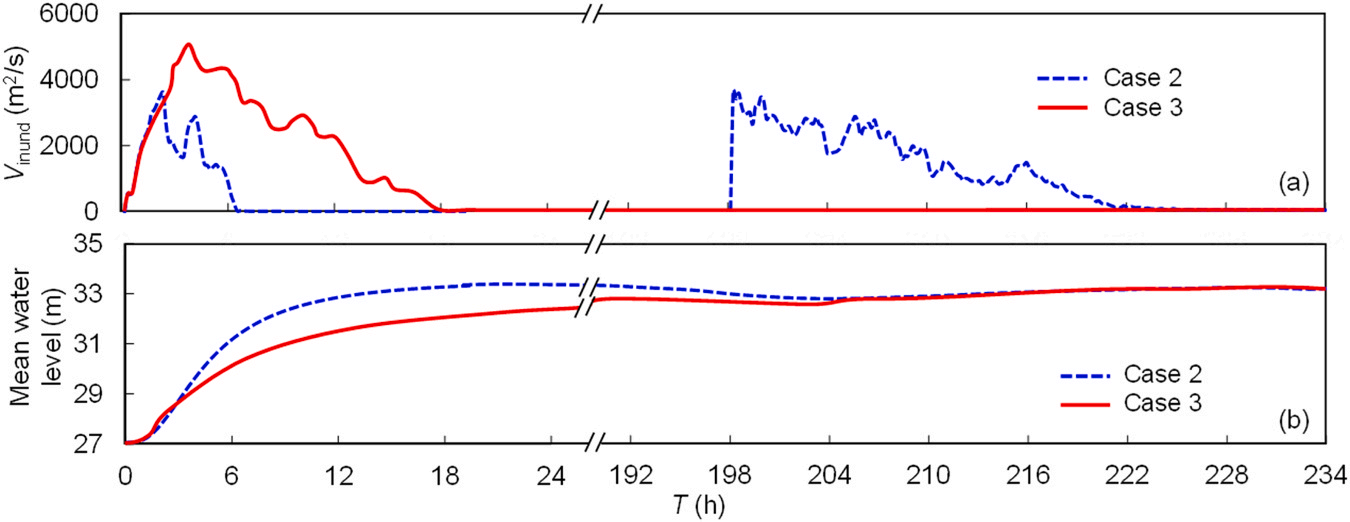
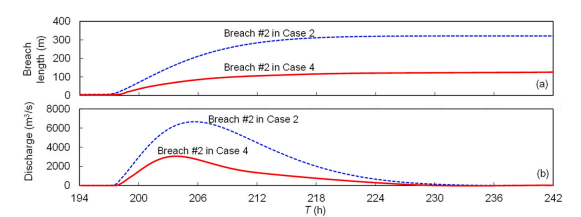
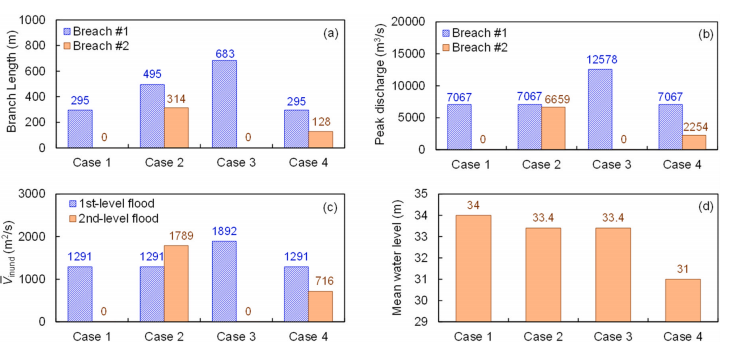
https://doi.org/10.1016/j.ejrh.2025.102495 摘要 研究区域:中国长江中游洞庭湖地区 研究重点:本文旨在开发一种耦合多级堤防溃决与洪水演进的高效数值方法,用于模拟多级堤防级联失效全过程。以研究区域1996年与2024年两起典型事件为例,揭示堤防级联失效的灾害放大效应,量化多级堤防的缓冲作用,并评估应急减灾措施的有效性。 区域水文新见解:与2024年单堤防溃决相比,1996年二级级联堤防溃决的主因是溃口#1形成后洞庭湖水位持续上涨,加速了溃口扩展与洪水演进过程。第二级堤防溃决引发溃口#1的二次侵蚀扩张,致使其溃口宽度增大2倍且二级洪水破坏力更强。基于四种情景的减灾措施分析表明:及时封堵溃口#1可使溃口#2宽度减少2/3,最大淹没率降低1/3;及时加固第二级堤防可阻断或延缓多级堤防的级联失效,为应急救援提供有效时间。 研究背景 全球主要流域的填海造地与蓄滞洪区建设促进了多级堤防系统的形成,虽提升了防洪韧性,但增加了堤防级联失效的风险。目前,对于级联堤防失效的触发机制、灾害后果放大效应以及有效的减灾策略研究仍存在不足。 通过历史案例研究、实地调查和实验室试验,学者们揭示了包括漫顶、集中渗流、反向侵蚀、接触冲刷、流土和管涌等多种堤防失效机制。在堤防溃决洪水模拟方面,当前二维耦合方法的计算效率相对较低。此外,现有溃堤洪水分析多采用单阶段失效方法,忽略了多阶段溃决的级联效应及其放大灾害影响的潜力,仅依赖单阶段溃口模型会导致对洪峰流量及其相关风险的显著低估。 迄今为止,仍缺乏通过耦合多级溃口动态演变与溃堤洪水演进的高效方法,来模拟多级堤防系统级联失效全过程。为填补这一空白,本研究提出了一种有效数值方法,用于模拟由多级堤防连续溃决引发的级联洪水。本研究以洞庭湖地区的两个具体案例为基础,对不同级联失效情景进行了综合分析,重点关注多级溃口发展规律和洪水演进模式,并进一步量化了多级堤防区域级联洪水灾害缓解措施的有效性,为应急管理中的科学决策提供理论依据。 研究区域和历史灾害回顾 01 区域概况 图1(a)为洞庭湖区域水系图,图1(b)为团洲垸的多级堤防体系,一级堤防总长20.8千米,位于洞庭湖西北岸;二级堤防长14.35千米,是团洲垸与钱南垸的分界线;三级堤防位于钱南垸西侧,以保护相邻的新胜大垸。 图1 研究区域:(a)洞庭湖区域水系图;(b)团洲垸三级堤防系统 图2为通过无人机摄影测量获取的团洲垸一、二级堤防代表性横截面:堤顶高程分别为37米和36.5米,坡度在1:2.5至1:3之间。 图2 团洲垸两级堤防的横截面 图3为城陵矶水文站在1996年和2024年洪水事件的水位记录。这两次事件峰值水位均超过了33米的警戒水位,造成了2024年团洲垸一级堤防溃口,以及1996年的两级堤防溃口。 图3 城陵矶站水位时程曲线:(a) 2024年;(b) 1996年 02 历史堤防溃决事件 图4为2024年7月5日的洞庭湖团洲垸一级堤防溃决前后的光学影像。6日12时左右,溃口宽度达到226米,垸内平均水深约5米。8日22时溃口完全封堵,9日8时启动排水,至12日,报告46起二级堤防渗漏与管涌险情,未发生连续溃堤。 图4 2024年团洲垸一级堤防溃堤前(a)、后(b)光学遥感影像 图5为1996年7月19日一级、二级堤防溃决后的光学影像。19日,一级堤防溃决,溃口宽度达295米;20日,二级堤防发生管涌,溃口宽度达314米,同时,一级堤防溃口因洪水侵蚀最终扩展至495米。造成6.5万人受影响,17人死亡。直到8月14日洞庭湖退洪后开始两处溃口修复和排水。 图5 1996年团洲垸(a)一级、(b)二级堤防溃后光学遥感影像 数值模拟方法 01 基于侵蚀的堤防溃决模型 该模型包含三个关键点:土壤可蚀性、溃口流量和溃口几何形态。 土壤侵蚀速率采用Hanson和Simon在2001年提出的经验公式计算。本研究利用洞庭湖地区可用的土壤参数范围,计算出堤防地质条件. 本研究溃口流量计算采用宽顶堰流假定,并引入一个修正因子ksm以考虑下游水位的影响。溃口几何形态的演变过程被划分为四个阶段,如图6所示。 图6 堤防溃决过程的四个阶段 02 洪水演进模型 采用一个集成的数值模型EDDA进行模拟,模型的控制方程为浅水方程(SWE),采用有限体积法进行数值求解,如图7所示。 图7 有限体积法示意图 03 数值耦合框架 堤防溃决模型与洪水演进模型在同一程序中实现耦合计算,并在每个时间步长执行耦合操作,计算流程如图8所示。其计算流程如下:初始化设置溃口1的初始几何形态与下游水位;基于溃堤模型计算溃口1首时段流量Qin-1,作为洪水淹没模型的边界条件执行第一个区域洪水演进,得到溃口1下游水位Hdown-1和溃口2上游水位Hup-2。若多级堤防失效,则重复计算迭代。 图8 堤防级联失效模拟数值耦合框架流程图 数值模拟在NVIDIA GeForce RTX 4090D GPU上执行,DEM分辨率为10m,2024年案例(50 km²区域,12小时洪水演进)耗时0.5小时,1996年案例(200 km²区域,240小时洪水演进)耗时9小时。 本研究侵蚀参数Kd和τc采用反演法确定堤防地质条件,来使溃口流量与几何形态计算值与实测值吻合。根据2024年实测溃口形态,临界边坡角αc取48°。 结果 01 多级堤防溃决 (1)第一级堤防溃决 图9表明,若没有及时封堵,2024年溃口宽度会扩大至250米。相比之下,1996年溃口#1扩张速度更快,在36小时内达295米。 图9 溃口宽度发展:(a) 2024年案例;(b) 1996年案例 图10(a)、(b)表明,1996年溃口#1形状更宽,但侵蚀深度与2024年相似。溃口扩展速率差异的原因为洞庭湖水位影响,2024年溃口发生后水位呈现下降趋势;而1996年溃口处初始水位更高,且溃后水位持续上升。图11表明1996年溃口初始水位差比2024年更高。 图10 (a) 2024年溃口形态演变,(b) 1996年溃口#1形态演变,(c) 1996年溃口#2形态演变。T为第一次溃堤后的时间。 图11 2024年和1996年案例中溃口处的水位差 (2)第二级堤防溃决 图9(b)表明1996年溃口#2的扩张速率略大于溃口#1。溃口#2发生导致洞庭湖的水继续灌入团洲垸,引发了溃口#1的后续扩张,最终宽度达到495米。 图10(c)表明溃口#1在第一级堤防失效过程中侵蚀深度大于溃口#2,归因为溃口#2发生时洞庭湖水位较低以及钱南垸的高程高于团洲垸。图11表明溃口#2处的初始水位差小于溃口#1处,导致1996年溃口#2向下扩张速率较慢。 图12(a)表明,在第二级堤防溃口期间,溃口#1的流量曲线与溃口#2非常相似。图13表明,1996年溃口#2平均流速峰值更高但持续时间更短,表明二级溃口具有显著的破坏性影响。 图12 2024年和1996年(a)流量,(b)淹没区总流入量变化 图13 2024年和1996年溃口平均流速变化 02 溃堤洪水演进 (1)洪水演进 图14为2024年溃堤洪水演进过程。洪水从北向最南端流动大约需9小时,18小时后,平均淹没深度为4.5米,最大水深达约10米。此外,第二级堤防附近水深较大,导致了46起管涌和渗透事件发生。 图14 2024年案例的洪水演进 图15为1996年两级堤防溃口的洪水演进过程。溃口#1洪水在7小时内淹没团洲垸,二级堤防附近水深超过7米;二级堤防经过160小时后失效,溃口#2洪水在38小时内淹没钱南垸。 图15 1996年案例的洪水演进 淹没率定义为每秒淹没面积的增加量,如图16(a)所示。1996年一级堤防溃口后最大淹没率约为2024年的两倍,归因于1996年溃口流量更大。1996年二级堤防溃决后平均淹没率是一级堤防溃决后的1.4倍,表明二级堤防溃决破坏力更强。 图16 . 2024年和1996年案例 (a)淹没率,(b)团洲垸平均水位变化 (2)水位变化 如图16(b)所示,1996年洞庭湖水位更高,溃口流量更大,导致团洲垸平均水位上升更为迅速。溃口#2发生后,部分水涌入钱南垸,致使团洲垸平均水位下降,其最终与钱南垸和洞庭湖水位持平。 讨论 利用1996年案例的水文条件和初始溃口形状,进一步比较了四种情景,如图17所示:(1)溃口#1发生时,二级堤防得到加固并保持稳定;(2)溃口#2在溃口#1关闭前发生;(3)溃口#1发生时没有二级堤防;(4)溃口#2在溃口#1关闭后发生。 图17 四种情景示意图 (1)多级堤防的缓冲作用 图18、19表明,案例3中的最终溃口宽度比案例2长188米,溃口#1的峰值流量增加了1.8倍。与1996年案例相比,没有二级堤防时洪水淹没没有间断,洪水以更快速度淹没更大区域。 图22中案例3与其他案例对比表明,多级堤防系统在时空尺度上对堤防溃决和洪水演进具有缓冲作用。即使发生级联失效,多级堤防的存在也能显著减少溃口规模、流量和淹没速率。 图18 有、无二级堤防下(a)溃口宽度和(b)流量变化 图19 有、无二级堤防下(a)淹没率和(b)团洲垸平均水位变化 (2)溃口#1封堵 图20、21表明,若溃口#1已被封堵,溃口#2的扩张速度和持续时间大大降低,且其发展不再影响溃口#1。案例4中溃口#2峰值流量减少到案例2的2/3,表明及时封堵溃口#1可以有效降低二级堤防溃口时的破坏力。 图22中案例2和4对比表明关闭先前溃口对后续级联失效的缓解作用。关闭溃口#1可以减小溃口#2的宽度和流量,降低淹没率和水位,从而缓解淹没区域的洪水风险。 图20 溃口1#封堵/不封堵情况下溃口#2的(a)溃口宽度和(b)流量变化 图21 溃口1#封堵/不封堵情况下溃口#2的(a)淹没率,(b)二级洪水下团洲垸平均水位变化 图22 四种工况下(a)溃口宽度,(b)洪峰流量,(c)平均淹没率和(d)团洲垸平均水位变化 (3)第二级堤防加固 图22表明,由于二级堤防失效,溃口#1宽度增加2倍,平均淹没率增加1.4倍。因此,当一级堤防出现溃口时,立即加固二级及其他级别的堤防至关重要。2024年案例自7月5日起开始对二级堤防进行加固,包括堆叠沙袋以保护坡脚、铺设防水布以防止雨水渗入等。 (4)排水 排水是应急救援中的一个关键环节。排水缓慢会使水更容易渗入堤防主体,可能导致堤防主体土壤恶化并引发管涌和新的溃口。然而,排水过快也可能导致堤防坡脚不稳定,引发滑坡、堤顶坍塌和突发性洪水等灾害链。为了揭示排水速率对堤防稳定性及潜在灾害链的影响,需进行系统的物理试验和数值模拟,这将是未来研究中一个非常重要的课题。 结论 本文以团洲垸两次溃堤事件为基准案例,研究了多级堤防溃决引发的洪水灾害。通过现场调查和数值模拟的综合分析,得出以下结论: (1)提出了一种新的耦合数值模拟方法,用于模拟多级堤防系统的级联失效过程。通过团洲垸1996年和2024年案例的现场记录数据验证了该方法的准确性。针对200km2区域,该方法计算时长仅为实际洪水持续时间的1/20,为应急救援决策提供高效支撑。 (2)通过两个案例的数值综合评估,揭示了1996年两级级联堤防失效的主要原因是溃口#1形成后洞庭湖水位持续上升,加速了溃口扩展并缩短了洪水演进过程,最终加剧了级联失效灾害后果。 (3)基于对1996年和2024年案例的全过程模拟,量化了堤防级联失效的灾害放大效应。二级堤防失效引发了溃口#1的后续侵蚀和扩展,导致溃口宽度增加2倍、深度增加1.05倍。这些结果强调了进行级联失效模拟的必要性,以解决传统单级溃堤模拟方法对灾害后果的低估问题。 (4)通过四种灾害情景的对比分析,为应急救援提供关键依据。二级堤防的存在使溃口#1的溃口宽度减小了188米,相应的峰值流量降低1.8倍。及时封堵溃口#1可有效将溃口#2的宽度减少2/3,最大淹没率降低1/3。及时加固二级堤防能够阻断或延迟多级堤防的级联失效,为应急救援争取时间。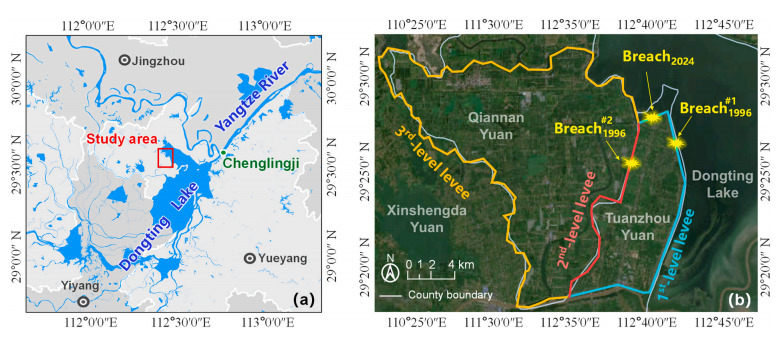


 成功提示
成功提示
 错误提示
错误提示
 警告提示
警告提示
评论 (0)