土方调配是土木工程中一项非常重要的工作，在一些大型工程建设中，土方调配的优劣直接决定了建设工程效益，显著影响工程建设的成本、进度、质量等各方面的进展，因此合理的土方调配方案能缩短工期、降低成本、提高建设项目的经济效益。尤其现在国家提倡建筑节能，这在一定程度上也响应了国家的号召，使建筑行业有效地避免了高能耗的尴尬局面。而在实际生产现场，许多施工人员仅凭自己积累的常识和经验粗略确定一个土方调配方案，然而不合理的土方调配方案容易造成土方的重复挖填和大量的土方运输，势必造成工程成本的提高。因此，找到科学有效的土方调配方法对土方施工具有一定的积极意义。本文将重点介绍表上作业法和MATLAB软件两种确定土方调配方案的方法，通过比较找到一种科学有效的方法，使得确定的土方调配方案满足土方总运输费用或使土方总运输量最少，从而达到降低工程成本的目的。

 

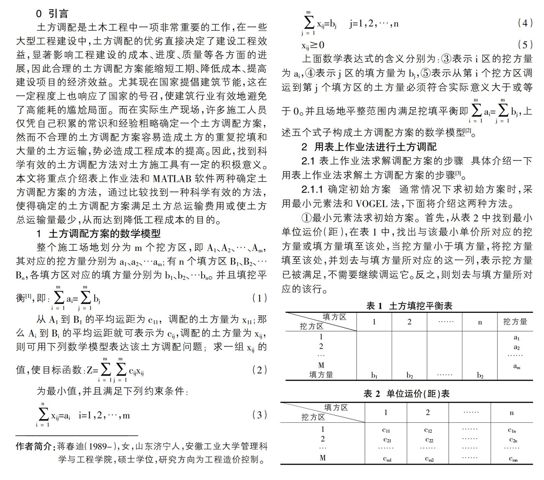
　　1土方调配方案的数学模型

 

　　2用表上作业法进行土方调配

 

　　2.1表上作业法求解调配方案的步骤具体介绍一下用表上作业法求解土方调配方案的步骤[3]。

 

　　2.1.1确定初始方案通常情况下求初始方案时，采用最小元素法和VOGEL法，下面将介绍这两种方法。

 

　　①最小元素法求初始方案。首先，从表2中找到最小单位运价（距），在表1中，找出与该最小单价所对应的挖方量或填方量填至该处，当挖方量小于填方量，将挖方量填至该处，并划去与填方量所对应的这一列，表示挖方量已被满足，不需要继续调运它。反之，则划去与填方量所对应的该行。

 

　　再者，除去划去的行或列，依据单位运价（距）中未被除去的单价（运距）中找寻最小的单价（或运距），然后重复第一步的步骤，重复进行此项工作，直到单位运价（距）表上所有数字都被划掉，此时可得到一个初始调运方案。

 

　　②VOGEL法确定初始方案。最小元素法确定初始方案时首先考虑最小单价（或最小运距），因此，往往为了节省一处的运费，造成其他处多花几倍的运费，因而并不能达到节省施工费用的目的。伏格尔法是这样考虑问题的，假如某一调配区的土方不能按最小单价（或最小运距）就近供应，就考虑次小单价（次小运距），最小单价（或最小运距）和次小单价（次小运距）有一个差额，差额越大，说明如果不能按最小单价调运时，那么土方运费增加的就越多。所以在两者差额最大的地方，用最小单价进行调运，避免运费增加的速度过快。伏格尔法确定初始调配方案的步骤是[5]：

 

　　第一步：在单位运价（距）表上的右端或下端，将各行各列的次小单价与最小单价作差，将计算的结果填入对应的行的右端或列的下端。

 

　　第二步：从单位运价（距）表中找到两者差值最大的行或列，从差值最大的行或列中找到最小单价（运距），然后确定土方调配的方向和数量。

 

　　第三步：当挖方区或填方区中，有一方数量上供应完毕或得到满足时，将单位运价表中对应的行或列划去。

 

　　第四步：重复上面的操作，直到单位运价（距）表中所有的元素都被划掉。

 

　　由以上可见，往往用伏格尔法确定的初始方案比用最小元素法确定的初始方案更接近最优方案。因此，在确定初始方案时，一般宜优先采用伏格尔法进行求解。

 

　　2.1.2最优解的判别用最小元素法和伏格尔法确定的方案只是初始方案，还要对该方案进行判别，如果没有达到理想值，还需要将其进行调整，进行优化，下面介绍两种优化初始方案的方法。

 

　　①闭回路法。确定的初始调配方案计算表中，从某个空格处出发，沿着水平或垂直方向用直线向前划，每碰到一个数字格就转90°，直到回到起始空格，形成一个闭回路。在闭回路上，从空格位置开始，按前进的方向的顶点依次用自然数标号。用闭回路法求非奇变量的检验数的具体方法是：对每个非基变量xij，其检验数？啄ij为：

 

　　？啄ij=（闭回路上的奇数次顶点单位运费之和）-（闭回路上的偶数次顶点单位运费之和）。

 

　　②位势法。用闭回路求检验数时，需给每一空格找闭回路，然后求空格处的检验数。若场地施工面积很大，挖方区和填方区比较多，计算过程会很繁琐。用位势法求各空格处的检验数比较简单，其步骤如下：

 

　　第一步：将初始方案中有调配数方格的Cij（单位运距或单位运价等）列出来；

 

　　第二步：按式⑥求出两组位势数ui（i=1，2，…m）和vj（j=1，2，…n）。

 

　　cij=ui+vj（6）

 

　　第三步：求出各个位势数后，便可依据式⑦求解各空格的检验数：？姿ij=cij-ui-vj（7）

 

　　第四步：如果空格处的检验数全部为非负，则为最优方案；如为负数则需进一步调整。

 

　　2.1.3解的改进方法—闭回路方法调整若存在空格检验数小于0，则该调运方案不是最优方案，还需要进行调整，调整的方法如下：①找闭回路。以最小的负检验数对应的非基变量为起始顶点在运量表中寻找一个闭回路。②求调整量。闭回路上偶数次顶点运量的最小值为调整量，记作：？兹。③调整。闭回路上的偶数次顶点的调运量减去？兹；闭回路上的奇数次顶点的调运量加上？兹；非闭回路顶点的其他变量调运量不变；再去掉闭回路上的一个0运量。

 

　　2.2表上作业法求解土方调配方案的最优流程综上所述，最小元素法确定初始方案时，往往为了节省某一处的运费，造成其他地方花费更多的成本，因而并不能达到减少施工成本的目的。由于VOGEL法得出的解在挖填区数量不多时往往为最优方案或挖填数量较多时可获得比较近似的解，所以此方法宜优先考虑采用。同时，后期对初始方案进行检验时，常用的方法有位势法和闭回路法。由于“位势法”的计算量要较闭回路法小得多，故也宜优先考虑采用。总之，将VOGEL法与位势法结合运用将会为土方调配运算提供很大的方便。

 

　　3用Matlab软件求解土方最优调配方案

 

　　从以上土方调配的数学模型可以看出，这属于土方调配在线性规划中的运输问题。Matlab软件包具有最优化工具箱，可以求解各类问题，尤其对线性规划问题的求解，利用Matlab的最优化工具箱可以方便实现。下面具体介绍一下如何用Matlab求优化解[6]。

 

　　有m个挖方区的挖方量ai和n个填方区的填方量bj合并组成的列向量用B表示。设：

 

　　将以上命令带入Matlab计算器，可以得到运行结果。

 

　　4表上作业法和Matlab软件求解最优土方调配方案的比较

 

　　以下一个具体算例通过Matlab软件和表上作业法分别求解土方调配方案，看哪种方法更具有实践准确性。

 

　　算例：某项施工队对施工场地进行平整，将填方区分为I、II、III、IV四个区，挖方区分为A、B、C三个区，各区间的单位运价及土方挖填量如表3所示。

 

　　4.1用表上作业法确定土方调配方案用表上作业法求初始方案时，一般宜采用VOGEL法，这样确定的初始方案跟最优方案比较接近。用VOGEL法确定的初始方案如表4所示，对应该初始方案的检验数如表5所示。

 

　　由表5可知，x24处的检验数为负，该初始方案不是最优，因此找出x24的闭回路，利用闭回路法对该初始方案进行调整，得到如表6所示的调配方案，对应该调整方案的检验数如表7所示。

 

　　由此可以看出，空格处的所有检验数均？叟0，故可知表7所示的方案为最优土方调配方案，此时调配土方的最小运输费用为：

 

　　minZ=9×300+8×1700+9×1300+10.5×200+11×400+10.5×2100=56550（元）

 

　　4.2用Matlab软件确定最优土方调配方案

 

　　针对该问题，用以下的Matlab命令可以方便的求解土方调配问题的经济优化解。

 

　　此时，用Matlab软件确定的土方调配方案的最小运输费用为：

 

　　minZ=9×300+8×1700+9×1300+10.5×200+11×400+10.5×2100=56550（元）

 

　　用Matlab软件求解出的土方调配方案跟用表上作业法求解的土方调配方案，结果是一样的。但用表上作业法求解调配方案时，过程比较繁琐，计算比较复杂，当挖填方区比较多时，计算就更容易出错。尤其用闭回路法进行调整时，要经过多次调整才能得到最优调配方案。但用Matlab软件求最优调配方案时，计算速度较快，计算的结果跟表上作业法相比也较为精确。由此可见，用Matlab软件求解土方运输实际问题时，快而准确，这一方法的运用将为施工人员解决实际土方调配问题提供基本方法和思路。

 

　　5总结

 

　　针对土方调配，本文阐述了两种确定土方调配方案的方法，即表上作业法和Matlab软件求解法。用表上作业法确定初始方案时，本文重点阐述了VOGEL法和最小元素法两种求解初始方案的方法，通过对比发现，VOGEL法往往比最小元素法求解的初始方案更贴近最优方案，有可能确定的初始方案就是最优方案。因此本文提议优先采用VOGEL法确定初始方案。如果确定的初始方案达不到最优要求，还要进一步采用闭回路方法将其调整，直至方案最优。对于利用Matlab优化工具箱求解土方调配方案时，首先阐述了求解调配方案的模型，根据模型阐述求解土方调配方案的相关程序指令，通过一个算例，同时用两种方法求其调配方案，发现得到的调配结果是一样的，但用Matlab软件确定土方调配方案比用表上作业法简单，便于操作，而且精确性也较高。因此，在实际确定土方调配方案时，可以大胆采用Matlab软件来快速实现土方调配方案的优化。

 

　　参考文献：

 

　　[1]马南湘.数学建模在土木工程土方调配中的应用[J].广西大学学报（自然科学版），2003，28（增刊）：17-20.

 

　　[2]牛艳丽，惠彦涛.运筹学模型在土方调配中的应用[J].山西建筑，2007，33（13）：83-84.

 

　　[3]李长安，李新辉.表上作业法优化土方调配方案解析[J].河南水利与南水北调，2010，7.

 

　　[4]胡运权.运筹学[M].哈尔滨：哈尔滨工业大学出版社，1998.

 

　　[5]李春锋.“VOGEL”法——解决土方调配问题的好方法[J].河西学院学报，2003，4（2）：83-89.

 

　　[6]王升.土方经济调配方案的Matlab实现[J].山西建筑，2012，38（20）.