2025-10-16 3088 0
Large deformation analysis of granular materials with stabilized and noise-free stress treatment in smoothed particle hydrodynamics
采用光滑粒子流体动力学进行稳定且无噪声应力处理的颗粒材料大变形分析

摘要: 本文提出了一种新型光滑粒子流体动力学(SPH)模型,用于提高颗粒材料大变形分析的精度与稳定性。为消除岩土工程SPH应用中常见的失稳后过程伪应力场,本研究构建了创新的应力扩散项。通过重正化技术提出新型边界处理方法,为岩土工程应用提供具有一阶一致性的壁面边界条件,该方法能有效处理尖锐拐角等复杂几何形态。系列算例验证表明:该边界构造即使采用较粗颗粒分辨率仍能提升计算精度;应力扩散项可显著降低大变形下影响应力场的数值噪声,获得平滑应力分布。最终将所建SPH模型应用于颗粒流与隧道掌子面坍塌模拟,结果显示其与实验数据吻合良好且具有收敛性。 引言: 涉及大变形的地球物理流动与许多自然现象和工程应用密切相关,包括雪崩和岩崩、灾害防治中的泥石流、边坡稳定性中的滑坡、抗震设计中的土壤液化以及大坝维护中的内部侵蚀。数值分析是研究地球物理流动中渐进式破坏并预测其潜在灾难性后果的有力工具,然而自由表面的存在和极大的变形是此类流动建模的主要挑战。 在计算岩土力学中,最广泛使用的预测工具基于有限元和有限差分方法。这些方法在求解偏微分方程 (PDEs) 方面非常高效,并已广泛应用于岩土工程问题的研究。尽管基于网格的方法取得了成功,但网格的使用仍然带来一些数值上的困难,例如网格畸变和区域离散化,这阻碍了它们在大变形和自由表面问题中的应用,例如在颗粒流和颗粒材料的失效后分析中遇到的问题。网格再生技术为解决网格畸变问题提供了一种可能的解决方案,然而这计算成本高昂且并不总是实用。 与基于网格的方法相比,无网格方法为大规模变形问题提供了更有效的解决方案,其中消除了网格连接性。用于颗粒材料和岩土工程应用的无网格方法示例包括光滑粒子流体动力学 (SPH)、物质点法 (MPM)和粒子有限元法 (PFEM) 。其中,SPH 可以被视为一种真正的无网格、拉格朗日方法。在 SPH 中,物理域被离散为一组拉格朗日粒子,这些粒子携带宏观场属性,并随材料速度移动。粒子之间的相互作用由称为光滑核函数的权重函数控制。由于采用局部插值来评估每个粒子的场变量,因此不需要背景网格来积分控制偏微分方程。这些特性使得 SPH 非常适合于涉及高度非线性、自由表面和大变形的问题。 尽管 SPH 最初是由 Gingold and Monaghan和 Lucy为天体物理问题开发的,但在过去的几十年里,它已被应用于广泛的应用领域,包括流体动力学、固体断裂、多相流、土-水相互作用以及泥石流。SPH 在计算岩土力学中的应用始于 Bui et al.。在他们的工作中,采用相关联和非相关联塑性流动法则的弹性-理想塑性 Drucker-Prager 模型被成功地应用于 SPH 格式中,用于研究粘性土和非粘性土的破坏后流动。随后,各种严格的本构模型,如 Bingham 流动模型、率相关粘塑性模型、亚塑性模型、基于临界状态的本构模型和被纳入 SPH 框架中以模拟不同的流动行为。此外,也有若干研究致力于消除 SPH 在大变形岩土力学问题中的缺点,例如拉伸不稳定性,这些研究将 SPH 与其他方法相结合,例如 Taylor-Galerkin SPH和 Stress-Particle SPH。 在大多数现有的岩土工程 SPH 应用中,重点主要放在运动学预测上,并且与实验观察相比获得了令人满意的结果。然而,在分析应力分布时,在大变形下观察到高频短波长的振荡。类似于在流体弱可压缩 SPH 中观察到的压力波动,这种伪应力场影响了 SPH 方法的精度并降低了其预测能力,因为应力的准确预测对于一些实际应用(例如模拟泥石流对结构的影响)非常重要。Nguyen et al.最近提出的应力正则化技术通过在整个域上执行滤波器,以特定的时间频率重新评估和重新分配每个粒子的应力,为伪应力场提供了一种解决方案。 Nguyen et al. (2017) 建议使用移动最小二乘 (MLS) 插值进行应力正则化以实现一阶校正。在他们的工作中,正则化技术成功地过滤了应力场中的高频数值噪声。然而,在 SPH 中使用滤波技术的一个常见问题是,对于长时间模拟,场变量可能会被过度滤波,从而影响所模拟过程中涉及的物理机制。此外,滤波过程本身需要对整个域进行额外的粒子扫描,这计算成本昂贵,特别是对于大尺度问题。因此,有必要寻找一种替代方法来进行应力平滑,同时能够保持动量守恒和一致性。 与 SPH 相关的另一个重要问题是边界条件的处理。数值模拟的准确性和鲁棒性高度依赖于 SPH 模型中采用的边界条件的性能。对于 SPH 在岩土力学中的应用,最广泛使用的边界处理是 Bui et al. (2008) 提出的方法。在他们的工作中,对于边界附近的土体粒子,邻近边界粒子的应力值被设定为与该土体粒子相同,从而在固体边界附近给出局部均匀的应力分布。无滑移边界条件是通过如 Morris et al. (1997) 中所述为边界粒子构建人工速度来施加的。后续研究提出了对 Bui 边界条件的若干修正。Peng et al. (2015) 认为 Bui 对边界粒子应力的处理可能无法保证无穿透条件,并提议将边界粒子应力张量的对角分量取为所关注土体粒子的最大值,而非对角分量设定为相同;这确保了边界产生足够大的压力。Chalk et al.对同一问题提出了不同的修改,他们采用单层虚拟壁面粒子施加排斥力以确保无穿透条件。另一种可能的边界处理依赖于使用虚拟粒子和重正化技术。虚拟边界粒子的场量(例如应力、速度)通过 Shepard 校正核函数从其邻近的土体粒子外推,以给出零阶一致性。也值得提及 Douillet-Grellier et al.和 Zhao et al.在开发无边界粒子的应力边界条件方面的工作。他们处理的基本思想是通过在动量方程中包含一个额外的应力项来补全边界附近粒子的截断核支持。这种类型的 Dirichlet 壁面边界条件可以在需要边界应力时应用,例如在三轴试验、巴西试验和硬币状裂纹问题的模拟中。 可用于 SPH 岩土工程应用的边界处理技术最多只能确保达到零阶一致性。边界处理中一致性的缺乏可能导致边界附近应力场的预测不佳。此外,尽管许多这些边界方法在简单几何形状的测试案例中表现良好,但它们的性能尚未在更复杂的几何形状下进行评估。 本工作开发了一种新方法,可以最小化 SPH 模拟岩土力学问题中常见的伪应力场,并解决现有边界条件的一些局限性。受流体动力学中密度扩散方案的启发,该方案提供了一种一致的数值算法来消除压力噪声和提高稳定性,本研究考虑了扩散过程以改进应力场。为了精确解析边界附近的应力分布同时能够处理复杂几何形状,本研究对 Marrone et al.提出的固定鬼粒子技术进行了修改来处理壁面边界条件。据作者所知,这是此类边界技术首次扩展到在 SPH 中模拟带应力的弹塑性固体。与 Marrone et al.中使用 MLS 插值来评估流动量不同,本文采用 Liu and Liu (2006) 提出的修正 SPH 插值来恢复边界处的一阶一致性。此过程可以在单个循环内实现,从而最大限度地减少计算成本。 本文剩余部分组织如下:第 2 节简要描述了控制方程和本构模型。随后,第 3 节给出了控制方程的 SPH 离散化以及数值扩散项的发展。第 4 节详细描述了一阶一致壁面边界处理。在第 5 节中,通过几个验证案例评估了新 SPH 方案的准确性和鲁棒性,包括库埃特流、简单剪切试验、带楔形体的静态土体、二维颗粒柱坍塌和隧道掌子面坍塌。最后,第 6 节给出了主要发现和结论。 图表:
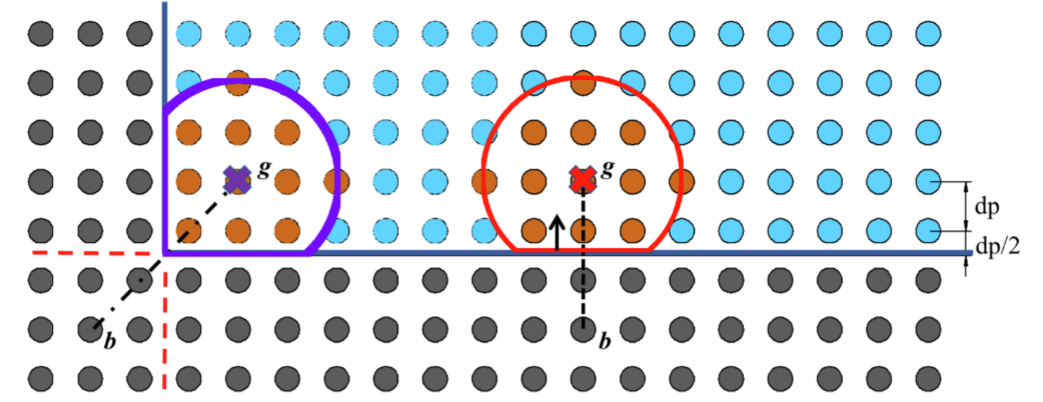
图1 平面与拐角处边界粒子(灰色圆圈)和鬼节点(十字标记)的生成示意图
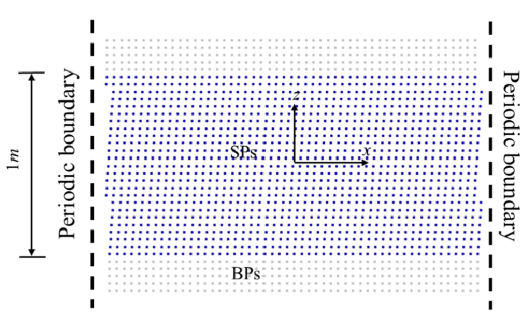
图2 库埃特流动算例的数值模型设置,其中土体粒子(SPs)标记为深蓝色,边界粒子(BPs)标记为浅灰色
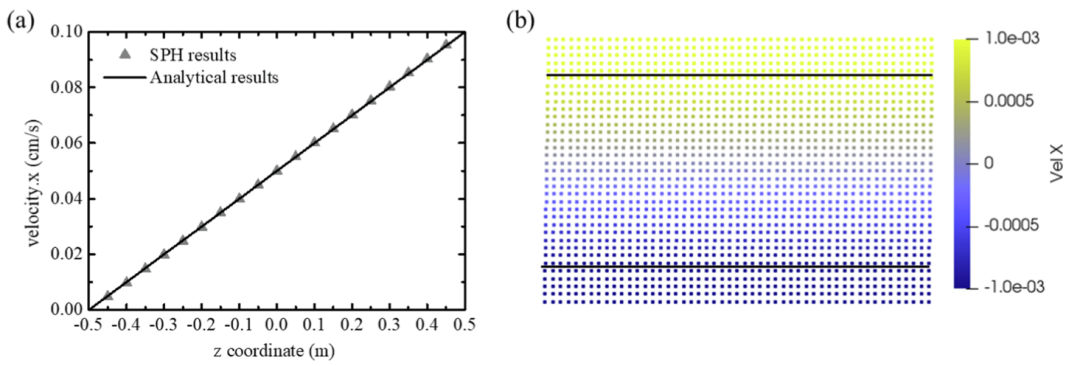
图3 库埃特流动的速度分布:(a) 与解析解对比;(b) t = 5 s时刻的速度云图(单位:m/s)
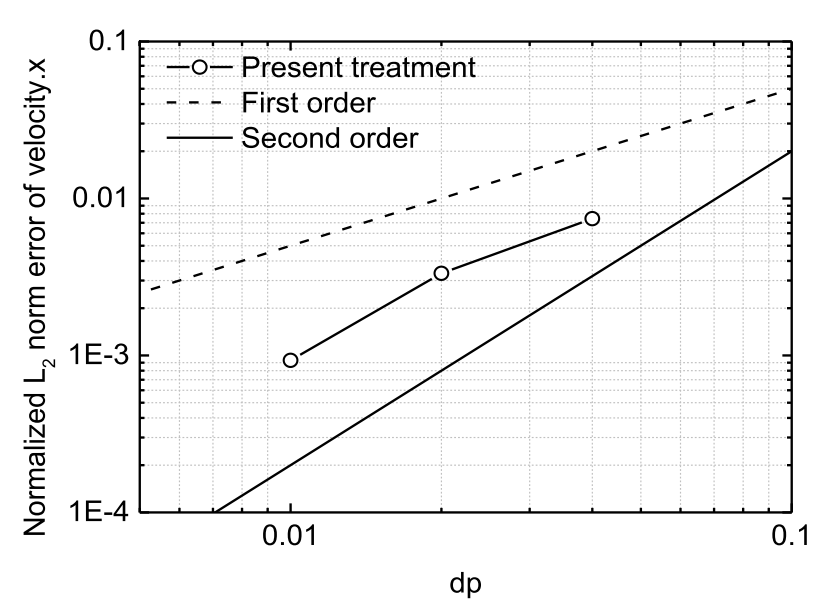
图4 库埃特流动在 t = 5 s 时速度的归一化 L2 误差范数
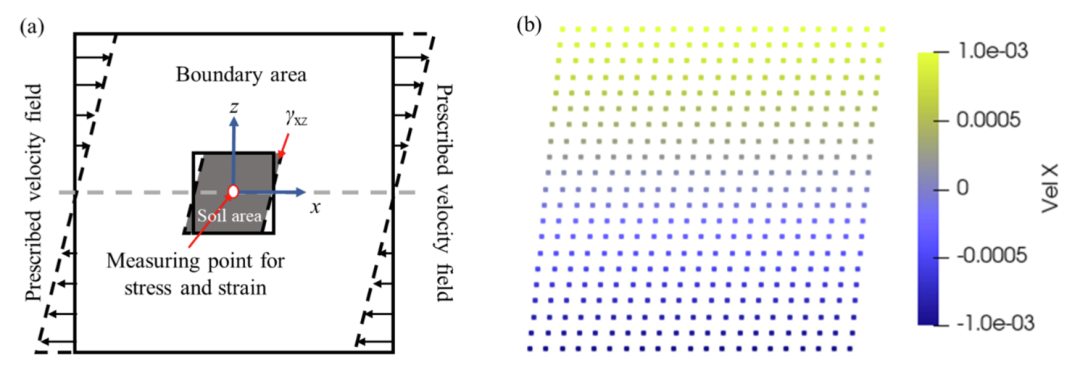
图5 用于测试SPH中Drucker-Prager弹塑性模型的简单剪切实验:(a) 模型设置;(b) 获得的流速分布图
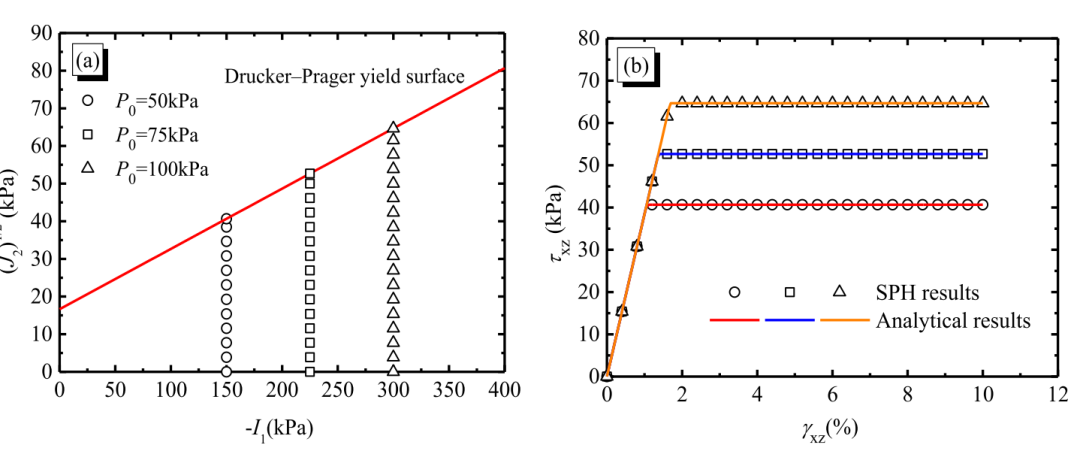
图6 不同围压条件下简单剪切试验的结果:(a) 应力路径;(b) 剪应力-应变关系曲线
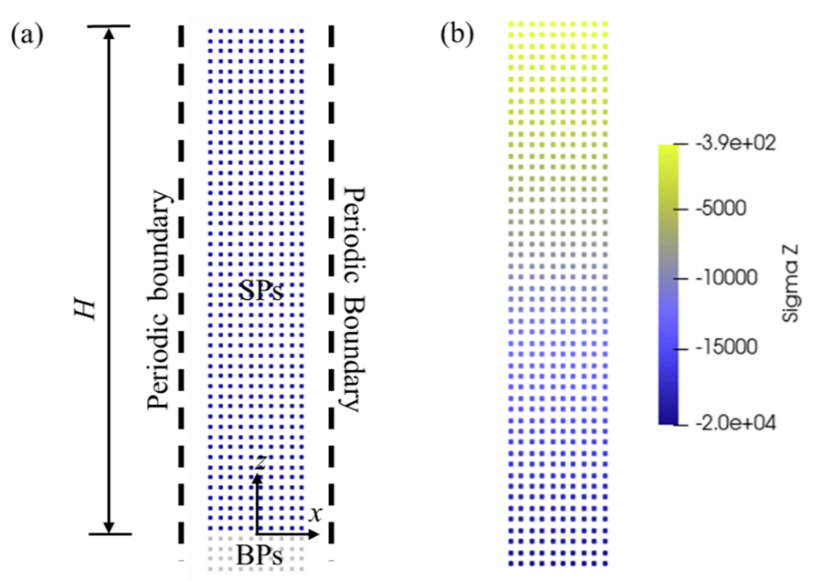
图7 静态土柱 (a) 模型设置,其中土体粒子和边界粒子分别标记为深蓝色和浅灰色;(b) 竖向应力云图
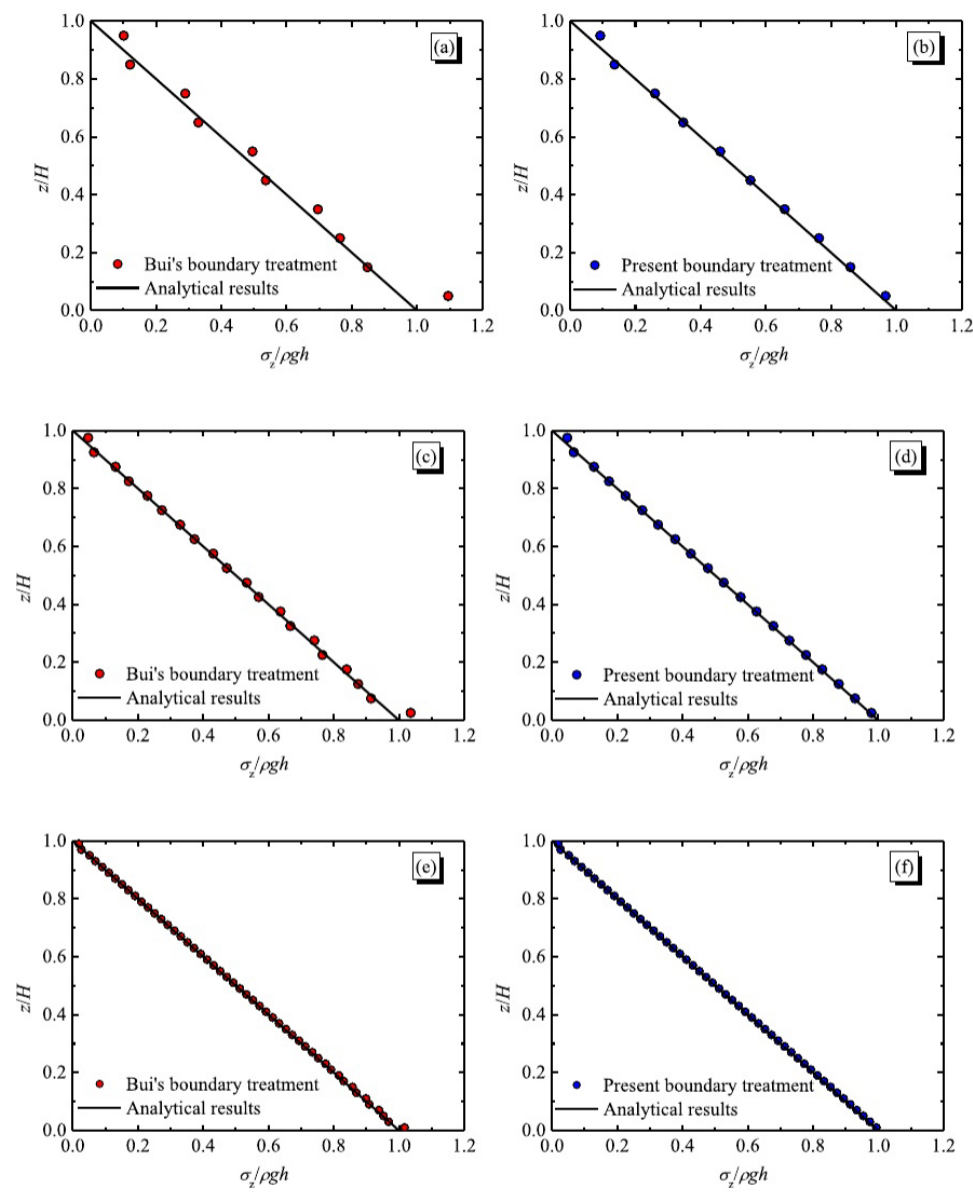
图8 在不同离散精度(dp = 0.1第一行,dp = 0.05第二行,dp = 0.02第三行)下最终时刻(t = 5 s)的归一化竖向应力分布对比
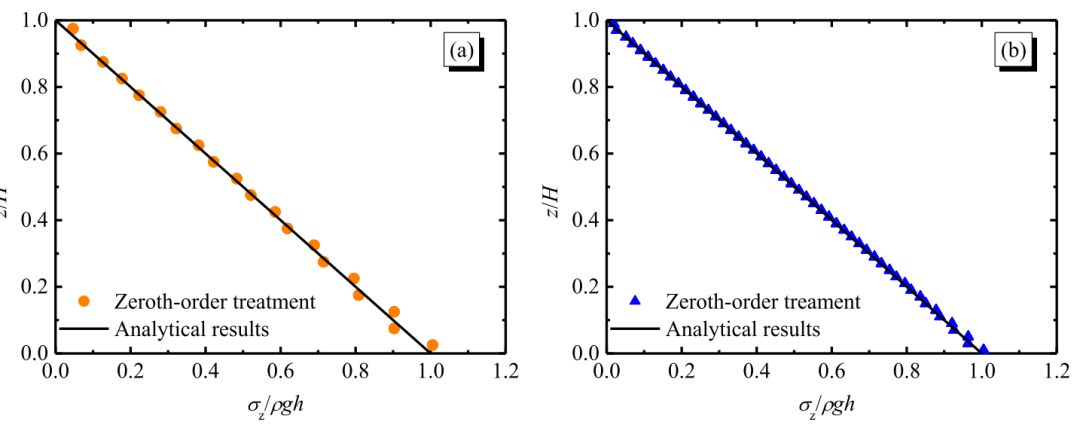
图9 采用零阶边界处理时的归一化竖向应力分布 (a) 粒子间距 dp = 0.05;(b) 粒子间距 dp = 0.02
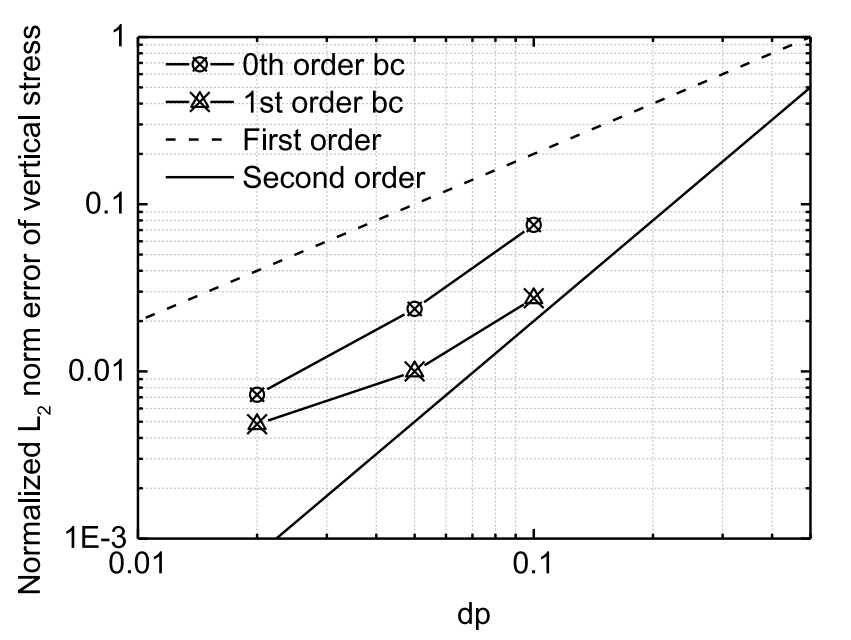
图10 静态土柱:5秒时刻竖向应力的归一化L2误差范数
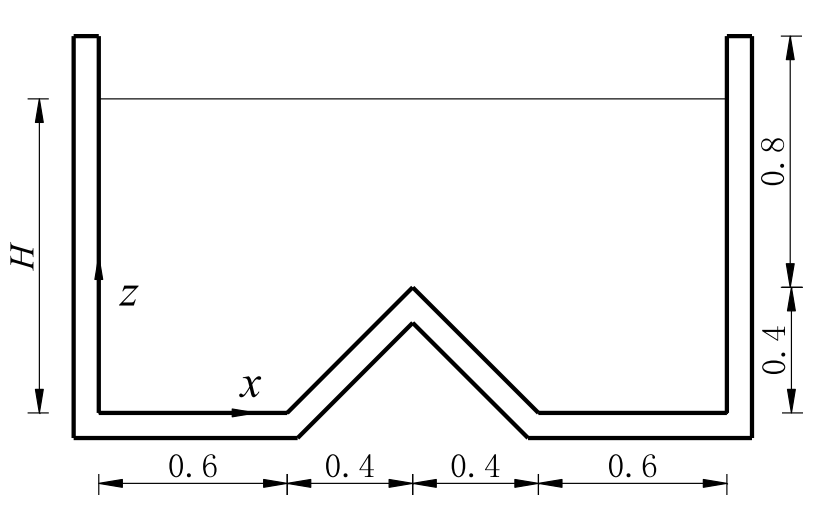
图11 带楔形容器内静态土体的示意图
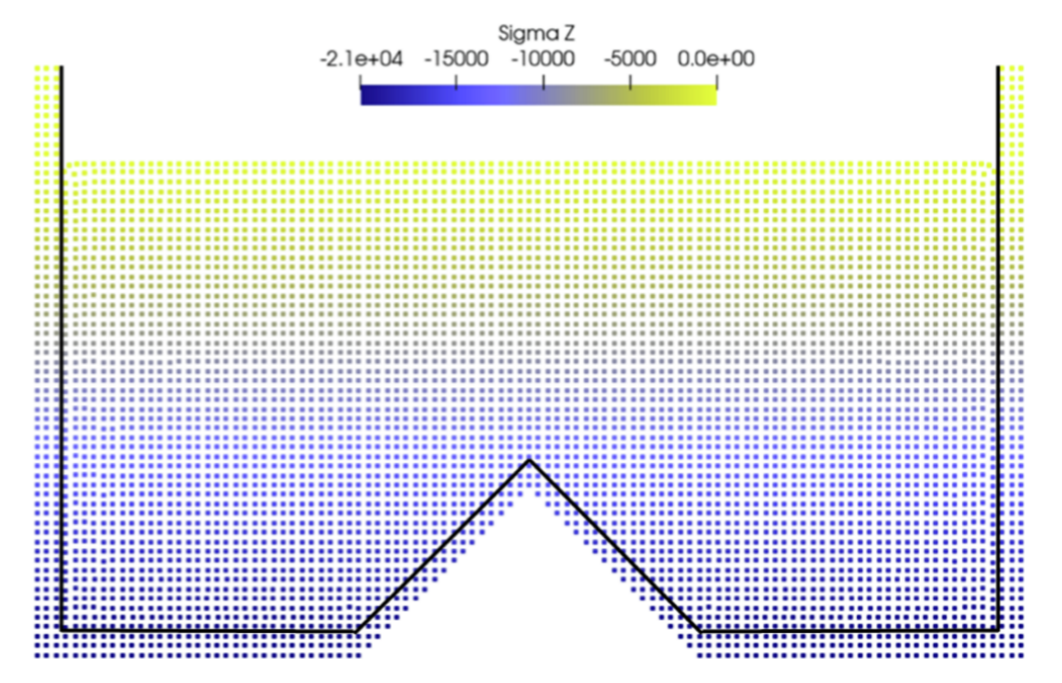
图12 含楔形体的静态干土:10秒时刻的归一化应力云图
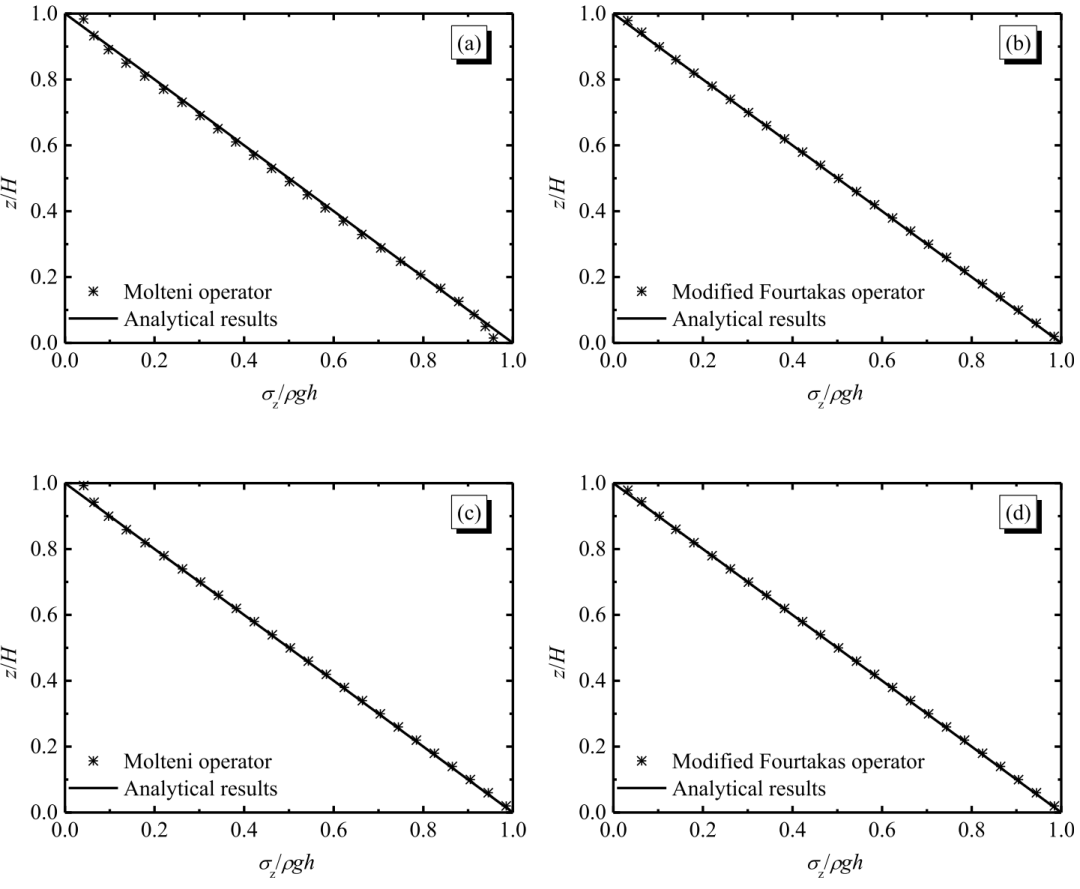
图13 含楔形体的静态干土:采用应力扩散项时在x=1.4m位置10秒时刻的归一化竖向应力分布。(a)和(b)未考虑边界对扩散项的贡献,(c)和(d)则考虑了边界贡献
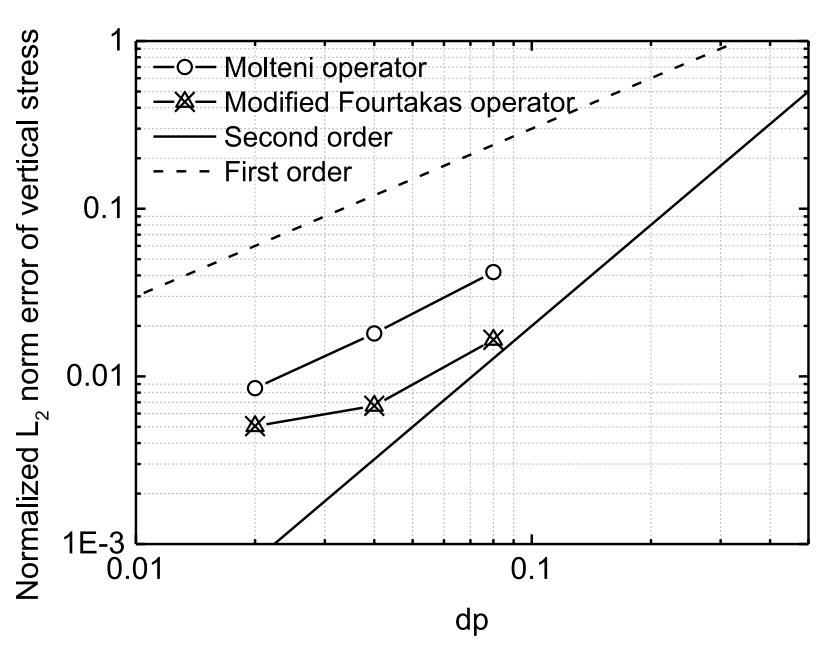
图14 含楔形体的静态干土:10秒时刻竖向应力的归一化L2范数误差
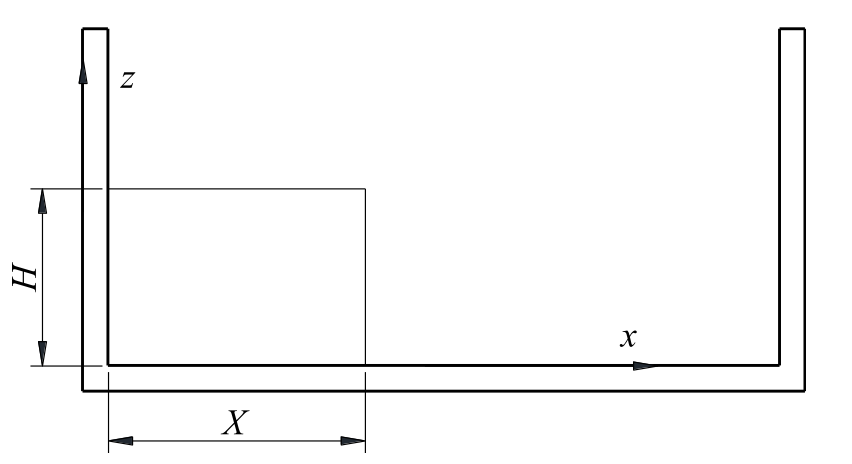
图15 颗粒柱坍塌问题的初始构型示意图
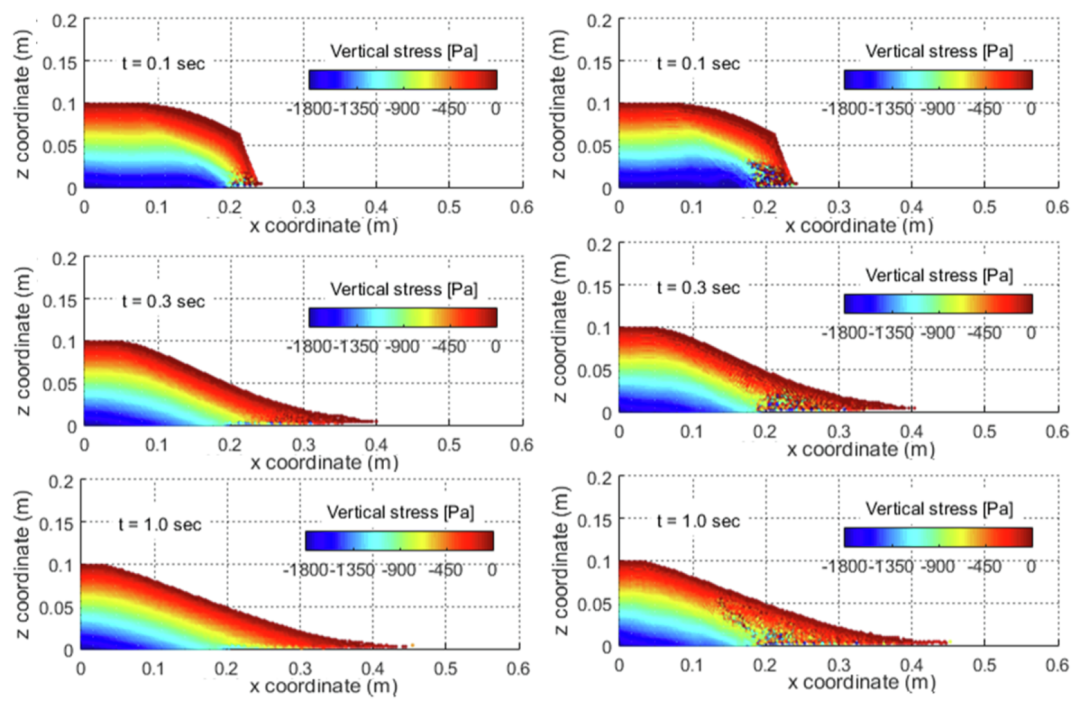
图16 二维颗粒流竖向应力云图:左列为采用扩散项的结果,右列为未采用扩散项的结果
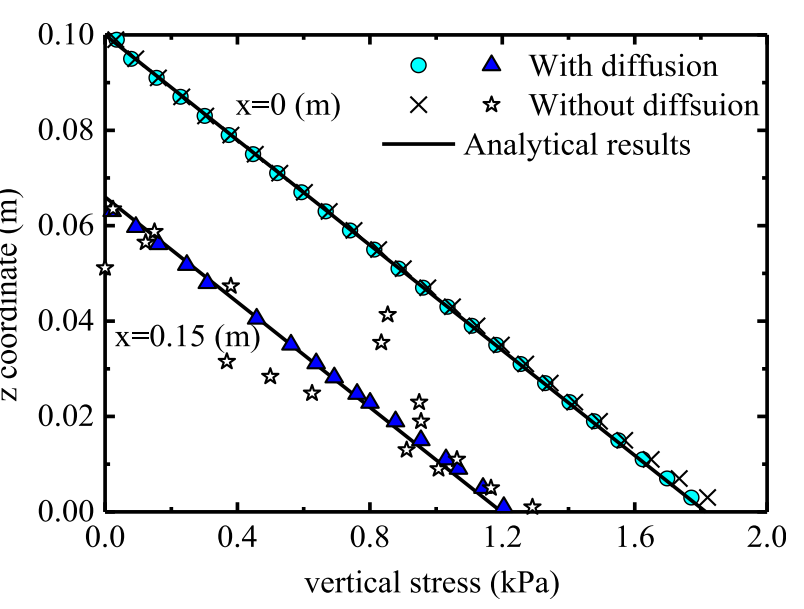
图17 最终堆积体的竖向应力分布
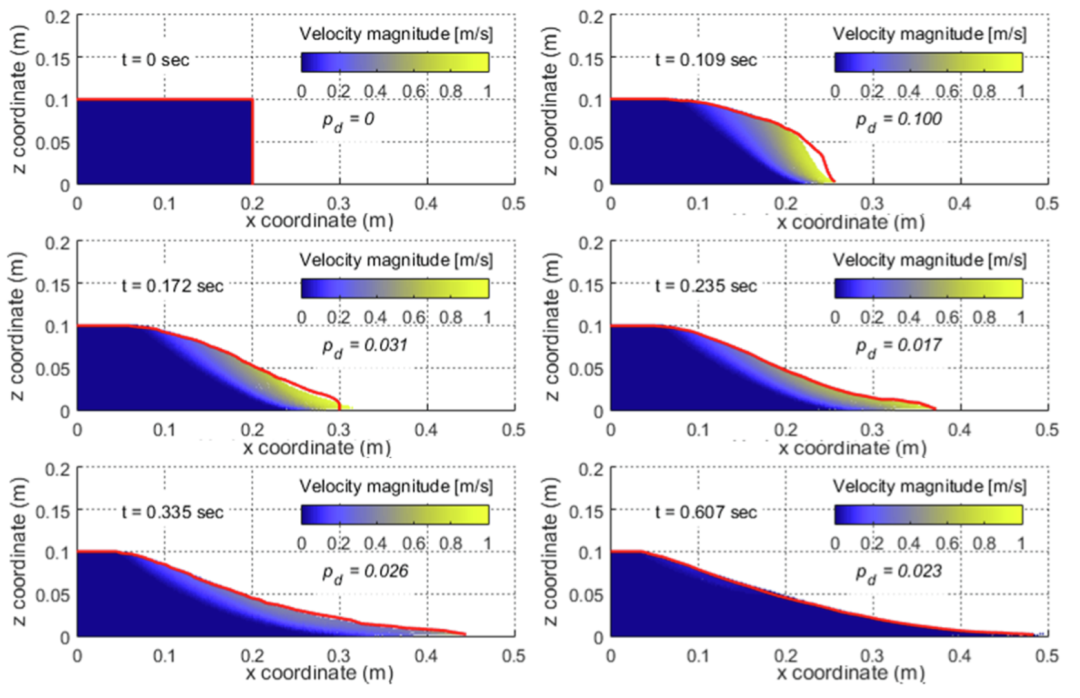
图18 二维颗粒柱坍塌过程的数值模拟与实验结果对比
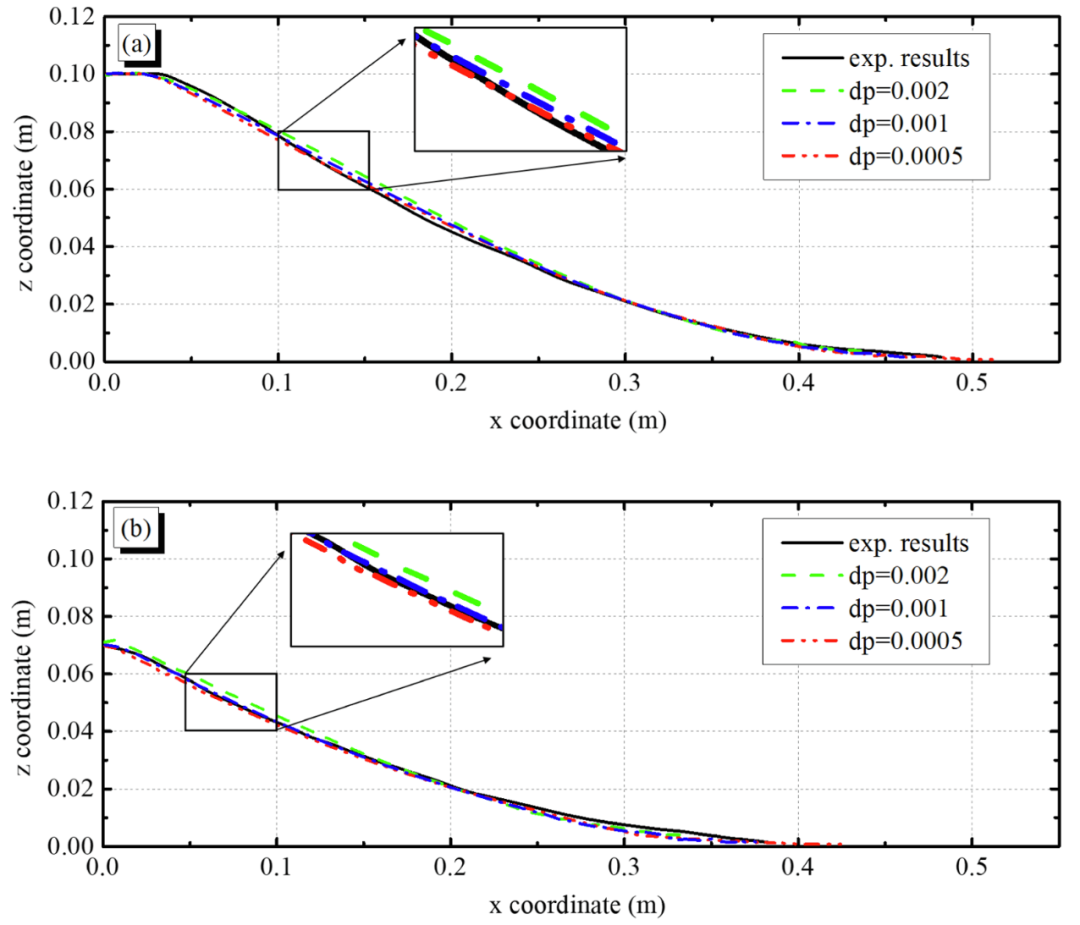
图19 SPH模拟与实验数据的自由表面线对比:(a) 长宽比a=0.5;(b) 长宽比a=1.0
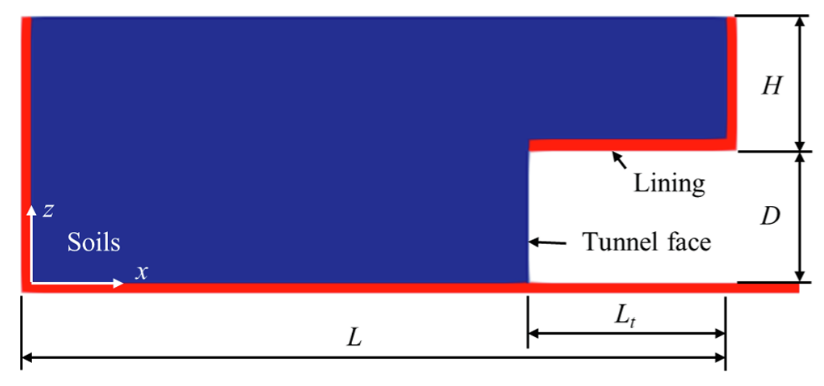
图20 隧道模型的计算设置(土体粒子与边界粒子分别标记为蓝色和红色)
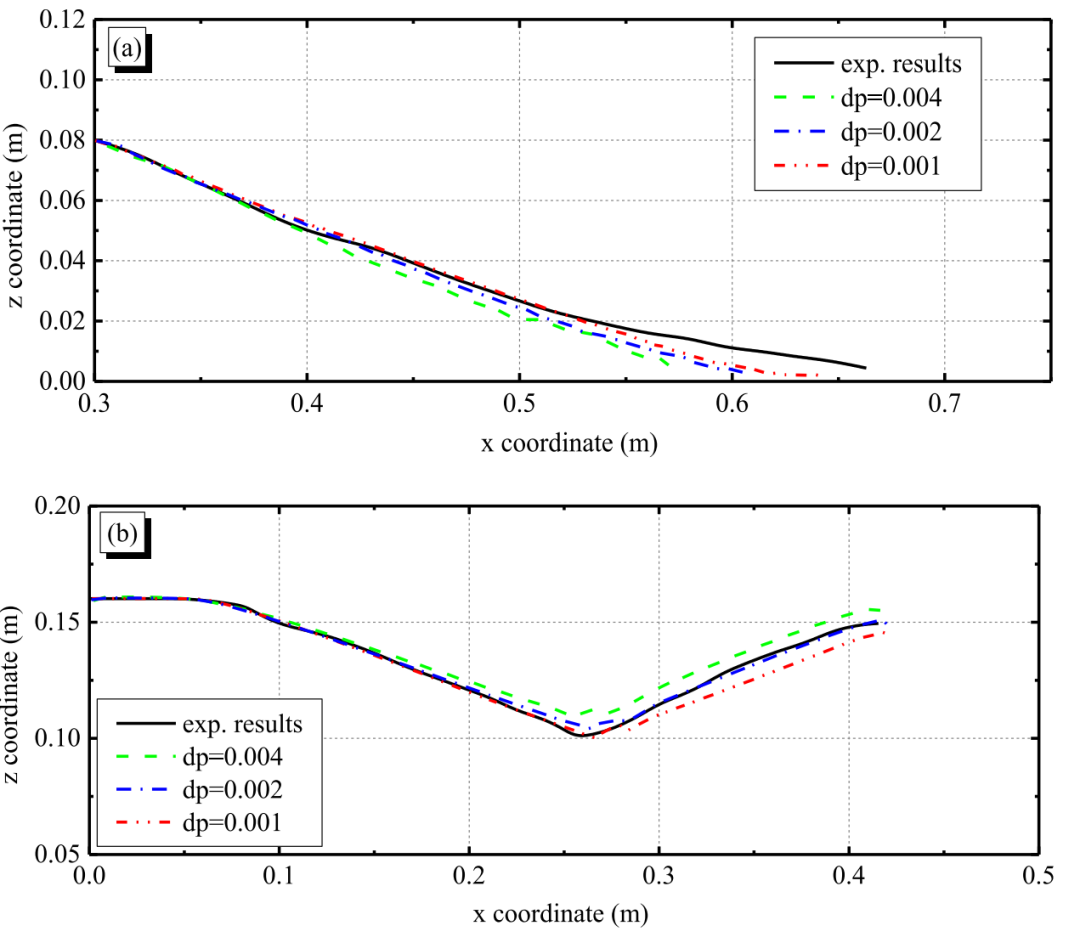
图21 与实验数据的对比(H/D = 1.0):(a) 掌子面挤出变形;(b) 地表沉降
结论: 本文提出了一种用于岩土材料大变形分析的新型SPH方法。引入了一种采用固定鬼粒子技术并结合一阶一致性插值的新型无滑移/自由滑移边界处理方法。此类边界方法在SPH解决岩土工程问题中的应用尚属首次。这种新的边界公式适用于复杂几何形状,并被证明能够提供精确的应力和速度预测。针对大变形下伪应力场这一SPH模拟岩土材料时的常见问题,提出了一种改进方案,即在应力中引入数值扩散项。本文讨论了几种构建扩散项的方法,并与新的扩散项算法进行了比较。结果表明,该算法能够在平滑数值噪声的同时,保持边界处的一致性。这种处理方法易于实现,且不需要额外的、成本高昂的应力插值过程。库埃特流、复杂几何形状中静态干土的模拟结果显示了速度和应力分布的收敛且精确的预测,证明了所提出技术的准确性、鲁棒性和适用性。该新方案最终被应用于颗粒柱坍塌和隧道掌子面坍塌的模拟,结果显示数值与实验结果高度吻合,并提供了平滑的应力场。 参考文献:
[1] Feng R, Fourtakas G, Rogers B D, et al. Large deformation analysis of granular materials with stabilized and noise-free stress treatment in smoothed particle hydrodynamics (SPH)[J]. Computers and Geotechnics, 2021, 138: 104356.
版权声明
本文仅用于学术交流与分享,版权属于原作者/出版商。文字翻译部分仅代表小编个人理解,如果错漏或侵权,请联系小编修改或删除。
Hot News
 成功提示
成功提示
 错误提示
错误提示
 警告提示
警告提示
评论 (0)